MATHHX B
\(\newcommand{\footnotename}{footnote}\)
\(\def \LWRfootnote {1}\)
\(\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#1}}}\)
\(\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}\)
\(\let \LWRorighspace \hspace \)
\(\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }\)
\(\newcommand {\mathnormal }[1]{{#1}}\)
\(\newcommand \ensuremath [1]{#1}\)
\(\newcommand {\LWRframebox }[2][]{\fbox {#2}} \newcommand {\framebox }[1][]{\LWRframebox } \)
\(\newcommand {\setlength }[2]{}\)
\(\newcommand {\addtolength }[2]{}\)
\(\newcommand {\setcounter }[2]{}\)
\(\newcommand {\addtocounter }[2]{}\)
\(\newcommand {\arabic }[1]{}\)
\(\newcommand {\number }[1]{}\)
\(\newcommand {\noalign }[1]{\text {#1}\notag \\}\)
\(\newcommand {\cline }[1]{}\)
\(\newcommand {\directlua }[1]{\text {(directlua)}}\)
\(\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}\)
\(\newcommand {\protect }{}\)
\(\def \LWRabsorbnumber #1 {}\)
\(\def \LWRabsorbquotenumber "#1 {}\)
\(\newcommand {\LWRabsorboption }[1][]{}\)
\(\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }\)
\(\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }\)
\(\def \mathcode #1={\mathchar }\)
\(\let \delcode \mathcode \)
\(\let \delimiter \mathchar \)
\(\def \oe {\unicode {x0153}}\)
\(\def \OE {\unicode {x0152}}\)
\(\def \ae {\unicode {x00E6}}\)
\(\def \AE {\unicode {x00C6}}\)
\(\def \aa {\unicode {x00E5}}\)
\(\def \AA {\unicode {x00C5}}\)
\(\def \o {\unicode {x00F8}}\)
\(\def \O {\unicode {x00D8}}\)
\(\def \l {\unicode {x0142}}\)
\(\def \L {\unicode {x0141}}\)
\(\def \ss {\unicode {x00DF}}\)
\(\def \SS {\unicode {x1E9E}}\)
\(\def \dag {\unicode {x2020}}\)
\(\def \ddag {\unicode {x2021}}\)
\(\def \P {\unicode {x00B6}}\)
\(\def \copyright {\unicode {x00A9}}\)
\(\def \pounds {\unicode {x00A3}}\)
\(\let \LWRref \ref \)
\(\renewcommand {\ref }{\ifstar \LWRref \LWRref }\)
\( \newcommand {\multicolumn }[3]{#3}\)
\(\require {textcomp}\)
\(\require {colortbl}\)
\(\let \LWRorigcolumncolor \columncolor \)
\(\renewcommand {\columncolor }[2][named]{\LWRorigcolumncolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\let \LWRorigrowcolor \rowcolor \)
\(\renewcommand {\rowcolor }[2][named]{\LWRorigrowcolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\let \LWRorigcellcolor \cellcolor \)
\(\renewcommand {\cellcolor }[2][named]{\LWRorigcellcolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\newcommand {\tothe }[1]{^{#1}}\)
\(\newcommand {\raiseto }[2]{{#2}^{#1}}\)
\(\newcommand {\LWRsiunitxEND }{}\)
\(\def \LWRsiunitxang #1;#2;#3;#4\LWRsiunitxEND {\ifblank {#1}{}{\num {#1}\degree }\ifblank {#2}{}{\num {#2}^{\unicode {x2032}}}\ifblank {#3}{}{\num {#3}^{\unicode {x2033}}}}\)
\(\newcommand {\ang }[2][]{\LWRsiunitxang #2;;;\LWRsiunitxEND }\)
\(\def \LWRsiunitxdistribunit {}\)
\(\newcommand {\LWRsiunitxENDTWO }{}\)
\(\def \LWRsiunitxprintdecimalsubtwo #1,#2,#3\LWRsiunitxENDTWO {\ifblank {#1}{0}{\mathrm {#1}}\ifblank {#2}{}{{\LWRsiunitxdecimal }\mathrm {#2}}}\)
\(\def \LWRsiunitxprintdecimalsub #1.#2.#3\LWRsiunitxEND {\LWRsiunitxprintdecimalsubtwo #1,,\LWRsiunitxENDTWO \ifblank {#2}{}{{\LWRsiunitxdecimal }\LWRsiunitxprintdecimalsubtwo
#2,,\LWRsiunitxENDTWO }}\)
\(\newcommand {\LWRsiunitxprintdecimal }[1]{\LWRsiunitxprintdecimalsub #1...\LWRsiunitxEND }\)
\(\def \LWRsiunitxnumplus #1+#2+#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxprintdecimal {#1}}{\ifblank {#1}{\LWRsiunitxprintdecimal {#2}}{\LWRsiunitxprintdecimal {#1}\unicode
{x02B}\LWRsiunitxprintdecimal {#2}}}\LWRsiunitxdistribunit }\)
\(\def \LWRsiunitxnumminus #1-#2-#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumplus #1+++\LWRsiunitxEND }{\ifblank {#1}{}{\LWRsiunitxprintdecimal {#1}}\unicode {x02212}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\def \LWRsiunitxnumpmmacro #1\pm #2\pm #3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumminus #1---\LWRsiunitxEND }{\LWRsiunitxprintdecimal {#1}\unicode {x0B1}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\def \LWRsiunitxnumpm #1+-#2+-#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumpmmacro #1\pm \pm \pm \LWRsiunitxEND }{\LWRsiunitxprintdecimal {#1}\unicode {x0B1}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\newcommand {\LWRsiunitxnumscientific }[2]{\ifblank {#1}{}{\ifstrequal {#1}{-}{-}{\LWRsiunitxprintdecimal {#1}\times }}10^{\LWRsiunitxprintdecimal {#2}}\LWRsiunitxdistribunit }\)
\(\def \LWRsiunitxnumD #1D#2D#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumpm #1+-+-\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumd #1d#2d#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumD #1DDD\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumE #1E#2E#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumd #1ddd\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnume #1e#2e#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumE #1EEE\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumx #1x#2x#3x#4\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnume #1eee\LWRsiunitxEND }{\ifblank {#3}{\LWRsiunitxnume #1eee\LWRsiunitxEND \times \LWRsiunitxnume
#2eee\LWRsiunitxEND }{\LWRsiunitxnume #1eee\LWRsiunitxEND \times \LWRsiunitxnume #2eee\LWRsiunitxEND \times \LWRsiunitxnume #3eee\LWRsiunitxEND }}}\)
\(\newcommand {\num }[2][]{\LWRsiunitxnumx #2xxxxx\LWRsiunitxEND }\)
\(\newcommand {\si }[2][]{\mathrm {\gsubstitute {#2}{~}{\,}}}\)
\(\def \LWRsiunitxSIopt #1[#2]#3{\def \LWRsiunitxdistribunit {\,\si {#3}}{#2}\num {#1}\def \LWRsiunitxdistribunit {}}\)
\(\newcommand {\LWRsiunitxSI }[2]{\def \LWRsiunitxdistribunit {\,\si {#2}}\num {#1}\def \LWRsiunitxdistribunit {}}\)
\(\newcommand {\SI }[2][]{\ifnextchar [{\LWRsiunitxSIopt {#2}}{\LWRsiunitxSI {#2}}}\)
\(\newcommand {\numlist }[2][]{\text {#2}}\)
\(\newcommand {\numrange }[3][]{\num {#2}\ \LWRsiunitxrangephrase \ \num {#3}}\)
\(\newcommand {\SIlist }[3][]{\text {#2}\,\si {#3}}\)
\(\newcommand {\SIrange }[4][]{\num {#2}\,#4\ \LWRsiunitxrangephrase \ \num {#3}\,#4}\)
\(\newcommand {\tablenum }[2][]{\mathrm {#2}}\)
\(\newcommand {\ampere }{\mathrm {A}}\)
\(\newcommand {\candela }{\mathrm {cd}}\)
\(\newcommand {\kelvin }{\mathrm {K}}\)
\(\newcommand {\kilogram }{\mathrm {kg}}\)
\(\newcommand {\metre }{\mathrm {m}}\)
\(\newcommand {\mole }{\mathrm {mol}}\)
\(\newcommand {\second }{\mathrm {s}}\)
\(\newcommand {\becquerel }{\mathrm {Bq}}\)
\(\newcommand {\degreeCelsius }{\unicode {x2103}}\)
\(\newcommand {\coulomb }{\mathrm {C}}\)
\(\newcommand {\farad }{\mathrm {F}}\)
\(\newcommand {\gray }{\mathrm {Gy}}\)
\(\newcommand {\hertz }{\mathrm {Hz}}\)
\(\newcommand {\henry }{\mathrm {H}}\)
\(\newcommand {\joule }{\mathrm {J}}\)
\(\newcommand {\katal }{\mathrm {kat}}\)
\(\newcommand {\lumen }{\mathrm {lm}}\)
\(\newcommand {\lux }{\mathrm {lx}}\)
\(\newcommand {\newton }{\mathrm {N}}\)
\(\newcommand {\ohm }{\mathrm {\Omega }}\)
\(\newcommand {\pascal }{\mathrm {Pa}}\)
\(\newcommand {\radian }{\mathrm {rad}}\)
\(\newcommand {\siemens }{\mathrm {S}}\)
\(\newcommand {\sievert }{\mathrm {Sv}}\)
\(\newcommand {\steradian }{\mathrm {sr}}\)
\(\newcommand {\tesla }{\mathrm {T}}\)
\(\newcommand {\volt }{\mathrm {V}}\)
\(\newcommand {\watt }{\mathrm {W}}\)
\(\newcommand {\weber }{\mathrm {Wb}}\)
\(\newcommand {\day }{\mathrm {d}}\)
\(\newcommand {\degree }{\mathrm {^\circ }}\)
\(\newcommand {\hectare }{\mathrm {ha}}\)
\(\newcommand {\hour }{\mathrm {h}}\)
\(\newcommand {\litre }{\mathrm {l}}\)
\(\newcommand {\liter }{\mathrm {L}}\)
\(\newcommand {\arcminute }{^\prime }\)
\(\newcommand {\minute }{\mathrm {min}}\)
\(\newcommand {\arcsecond }{^{\prime \prime }}\)
\(\newcommand {\tonne }{\mathrm {t}}\)
\(\newcommand {\astronomicalunit }{au}\)
\(\newcommand {\atomicmassunit }{u}\)
\(\newcommand {\bohr }{\mathit {a}_0}\)
\(\newcommand {\clight }{\mathit {c}_0}\)
\(\newcommand {\dalton }{\mathrm {D}_\mathrm {a}}\)
\(\newcommand {\electronmass }{\mathit {m}_{\mathrm {e}}}\)
\(\newcommand {\electronvolt }{\mathrm {eV}}\)
\(\newcommand {\elementarycharge }{\mathit {e}}\)
\(\newcommand {\hartree }{\mathit {E}_{\mathrm {h}}}\)
\(\newcommand {\planckbar }{\mathit {\unicode {x210F}}}\)
\(\newcommand {\angstrom }{\mathrm {\unicode {x212B}}}\)
\(\let \LWRorigbar \bar \)
\(\newcommand {\barn }{\mathrm {b}}\)
\(\newcommand {\bel }{\mathrm {B}}\)
\(\newcommand {\decibel }{\mathrm {dB}}\)
\(\newcommand {\knot }{\mathrm {kn}}\)
\(\newcommand {\mmHg }{\mathrm {mmHg}}\)
\(\newcommand {\nauticalmile }{\mathrm {M}}\)
\(\newcommand {\neper }{\mathrm {Np}}\)
\(\newcommand {\yocto }{\mathrm {y}}\)
\(\newcommand {\zepto }{\mathrm {z}}\)
\(\newcommand {\atto }{\mathrm {a}}\)
\(\newcommand {\femto }{\mathrm {f}}\)
\(\newcommand {\pico }{\mathrm {p}}\)
\(\newcommand {\nano }{\mathrm {n}}\)
\(\newcommand {\micro }{\mathrm {\unicode {x00B5}}}\)
\(\newcommand {\milli }{\mathrm {m}}\)
\(\newcommand {\centi }{\mathrm {c}}\)
\(\newcommand {\deci }{\mathrm {d}}\)
\(\newcommand {\deca }{\mathrm {da}}\)
\(\newcommand {\hecto }{\mathrm {h}}\)
\(\newcommand {\kilo }{\mathrm {k}}\)
\(\newcommand {\mega }{\mathrm {M}}\)
\(\newcommand {\giga }{\mathrm {G}}\)
\(\newcommand {\tera }{\mathrm {T}}\)
\(\newcommand {\peta }{\mathrm {P}}\)
\(\newcommand {\exa }{\mathrm {E}}\)
\(\newcommand {\zetta }{\mathrm {Z}}\)
\(\newcommand {\yotta }{\mathrm {Y}}\)
\(\newcommand {\percent }{\mathrm {\%}}\)
\(\newcommand {\meter }{\mathrm {m}}\)
\(\newcommand {\metre }{\mathrm {m}}\)
\(\newcommand {\gram }{\mathrm {g}}\)
\(\newcommand {\kg }{\kilo \gram }\)
\(\newcommand {\of }[1]{_{\mathrm {#1}}}\)
\(\newcommand {\squared }{^2}\)
\(\newcommand {\square }[1]{\mathrm {#1}^2}\)
\(\newcommand {\cubed }{^3}\)
\(\newcommand {\cubic }[1]{\mathrm {#1}^3}\)
\(\newcommand {\per }{\,\mathrm {/}}\)
\(\newcommand {\celsius }{\unicode {x2103}}\)
\(\newcommand {\fg }{\femto \gram }\)
\(\newcommand {\pg }{\pico \gram }\)
\(\newcommand {\ng }{\nano \gram }\)
\(\newcommand {\ug }{\micro \gram }\)
\(\newcommand {\mg }{\milli \gram }\)
\(\newcommand {\g }{\gram }\)
\(\newcommand {\kg }{\kilo \gram }\)
\(\newcommand {\amu }{\mathrm {u}}\)
\(\newcommand {\nm }{\nano \metre }\)
\(\newcommand {\um }{\micro \metre }\)
\(\newcommand {\mm }{\milli \metre }\)
\(\newcommand {\cm }{\centi \metre }\)
\(\newcommand {\dm }{\deci \metre }\)
\(\newcommand {\m }{\metre }\)
\(\newcommand {\km }{\kilo \metre }\)
\(\newcommand {\as }{\atto \second }\)
\(\newcommand {\fs }{\femto \second }\)
\(\newcommand {\ps }{\pico \second }\)
\(\newcommand {\ns }{\nano \second }\)
\(\newcommand {\us }{\micro \second }\)
\(\newcommand {\ms }{\milli \second }\)
\(\newcommand {\s }{\second }\)
\(\newcommand {\fmol }{\femto \mol }\)
\(\newcommand {\pmol }{\pico \mol }\)
\(\newcommand {\nmol }{\nano \mol }\)
\(\newcommand {\umol }{\micro \mol }\)
\(\newcommand {\mmol }{\milli \mol }\)
\(\newcommand {\mol }{\mol }\)
\(\newcommand {\kmol }{\kilo \mol }\)
\(\newcommand {\pA }{\pico \ampere }\)
\(\newcommand {\nA }{\nano \ampere }\)
\(\newcommand {\uA }{\micro \ampere }\)
\(\newcommand {\mA }{\milli \ampere }\)
\(\newcommand {\A }{\ampere }\)
\(\newcommand {\kA }{\kilo \ampere }\)
\(\newcommand {\ul }{\micro \litre }\)
\(\newcommand {\ml }{\milli \litre }\)
\(\newcommand {\l }{\litre }\)
\(\newcommand {\hl }{\hecto \litre }\)
\(\newcommand {\uL }{\micro \liter }\)
\(\newcommand {\mL }{\milli \liter }\)
\(\newcommand {\L }{\liter }\)
\(\newcommand {\hL }{\hecto \liter }\)
\(\newcommand {\mHz }{\milli \hertz }\)
\(\newcommand {\Hz }{\hertz }\)
\(\newcommand {\kHz }{\kilo \hertz }\)
\(\newcommand {\MHz }{\mega \hertz }\)
\(\newcommand {\GHz }{\giga \hertz }\)
\(\newcommand {\THz }{\tera \hertz }\)
\(\newcommand {\mN }{\milli \newton }\)
\(\newcommand {\N }{\newton }\)
\(\newcommand {\kN }{\kilo \newton }\)
\(\newcommand {\MN }{\mega \newton }\)
\(\newcommand {\Pa }{\pascal }\)
\(\newcommand {\kPa }{\kilo \pascal }\)
\(\newcommand {\MPa }{\mega \pascal }\)
\(\newcommand {\GPa }{\giga \pascal }\)
\(\newcommand {\mohm }{\milli \ohm }\)
\(\newcommand {\kohm }{\kilo \ohm }\)
\(\newcommand {\Mohm }{\mega \ohm }\)
\(\newcommand {\pV }{\pico \volt }\)
\(\newcommand {\nV }{\nano \volt }\)
\(\newcommand {\uV }{\micro \volt }\)
\(\newcommand {\mV }{\milli \volt }\)
\(\newcommand {\V }{\volt }\)
\(\newcommand {\kV }{\kilo \volt }\)
\(\newcommand {\W }{\watt }\)
\(\newcommand {\uW }{\micro \watt }\)
\(\newcommand {\mW }{\milli \watt }\)
\(\newcommand {\kW }{\kilo \watt }\)
\(\newcommand {\MW }{\mega \watt }\)
\(\newcommand {\GW }{\giga \watt }\)
\(\newcommand {\J }{\joule }\)
\(\newcommand {\uJ }{\micro \joule }\)
\(\newcommand {\mJ }{\milli \joule }\)
\(\newcommand {\kJ }{\kilo \joule }\)
\(\newcommand {\eV }{\electronvolt }\)
\(\newcommand {\meV }{\milli \electronvolt }\)
\(\newcommand {\keV }{\kilo \electronvolt }\)
\(\newcommand {\MeV }{\mega \electronvolt }\)
\(\newcommand {\GeV }{\giga \electronvolt }\)
\(\newcommand {\TeV }{\tera \electronvolt }\)
\(\newcommand {\kWh }{\kilo \watt \hour }\)
\(\newcommand {\F }{\farad }\)
\(\newcommand {\fF }{\femto \farad }\)
\(\newcommand {\pF }{\pico \farad }\)
\(\newcommand {\K }{\mathrm {K}}\)
\(\newcommand {\dB }{\mathrm {dB}}\)
\(\newcommand {\kibi }{\mathrm {Ki}}\)
\(\newcommand {\mebi }{\mathrm {Mi}}\)
\(\newcommand {\gibi }{\mathrm {Gi}}\)
\(\newcommand {\tebi }{\mathrm {Ti}}\)
\(\newcommand {\pebi }{\mathrm {Pi}}\)
\(\newcommand {\exbi }{\mathrm {Ei}}\)
\(\newcommand {\zebi }{\mathrm {Zi}}\)
\(\newcommand {\yobi }{\mathrm {Yi}}\)
\(\let \unit \si \)
\(\let \qty \SI \)
\(\let \qtylist \SIlist \)
\(\let \qtyrange \SIrange \)
\(\let \numproduct \num \)
\(\let \qtyproduct \SI \)
\(\let \complexnum \num \)
\(\newcommand {\complexqty }[3][]{(\complexnum {#2})\si {#3}}\)
\(\newcommand {\mleft }{\left }\)
\(\newcommand {\mright }{\right }\)
\(\newcommand {\mleftright }{}\)
\(\newcommand {\mleftrightrestore }{}\)
\(\require {gensymb}\)
\(\newcommand {\intertext }[1]{\text {#1}\notag \\}\)
\(\let \Hat \hat \)
\(\let \Check \check \)
\(\let \Tilde \tilde \)
\(\let \Acute \acute \)
\(\let \Grave \grave \)
\(\let \Dot \dot \)
\(\let \Ddot \ddot \)
\(\let \Breve \breve \)
\(\let \Bar \bar \)
\(\let \Vec \vec \)
\(\require {cancel}\)
\(\newcommand {\Dm }{\operatorname {Dm}}\)
\(\newcommand {\Vm }{\operatorname {Vm}}\)
\(\newcommand {\Var }{\operatorname {Var}}\)
\(\newcommand {\tcbset }[1]{}\)
\(\newcommand {\tcbsetforeverylayer }[1]{}\)
\(\newcommand {\tcbox }[2][]{\boxed {\text {#2}}}\)
\(\newcommand {\tcboxfit }[2][]{\boxed {#2}}\)
\(\newcommand {\tcblower }{}\)
\(\newcommand {\tcbline }{}\)
\(\newcommand {\tcbtitle }{}\)
\(\newcommand {\tcbsubtitle [2][]{\mathrm {#2}}}\)
\(\newcommand {\tcboxmath }[2][]{\boxed {#2}}\)
\(\newcommand {\tcbhighmath }[2][]{\boxed {#2}}\)
\(\newcommand {\toprule }[1][]{\hline }\)
\(\let \midrule \toprule \)
\(\let \bottomrule \toprule \)
\(\def \LWRbooktabscmidruleparen (#1)#2{}\)
\(\newcommand {\LWRbooktabscmidrulenoparen }[1]{}\)
\(\newcommand {\cmidrule }[1][]{\ifnextchar (\LWRbooktabscmidruleparen \LWRbooktabscmidrulenoparen }\)
\(\newcommand {\morecmidrules }{}\)
\(\newcommand {\specialrule }[3]{\hline }\)
\(\newcommand {\addlinespace }[1][]{}\)
\(\def \LWRsiunitxrangephrase { \protect \mbox {to (numerical range)} }\)
\(\def \LWRsiunitxdecimal {.}\)
3.5 Lineær regression i WordMat
OBS: Dette afsnit kan springes over, hvis du er på den gamle ordning (startet før 2024). I stedet skal du så læse afsnit 3.6.
Vi skal bruge et Excel-ark fra WordMat. Hvis du har WordMat installeret, finder du det her:
Hvis ikke du har WordMat installeret, kan du downloade arket her.
Øvelse 3.5.1
For at kunne følge med i resten har du brug for det omtalte Excel-ark.
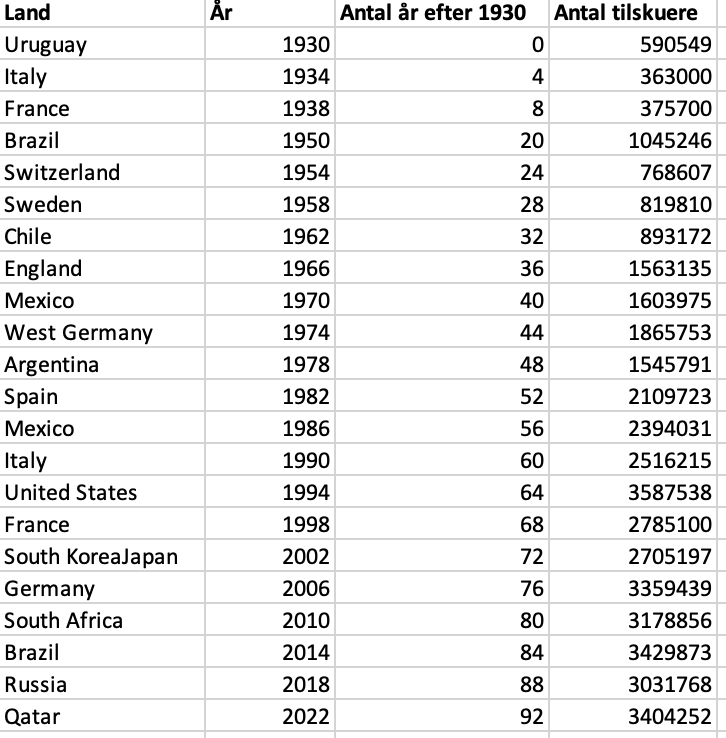
Lineær regression bruges til at beskrive udviklinger, som er tilnærmelsesvist lineære. Vi vil i det følgende kigge på tilskuerudviklingen ved VM i fodbold i perioden 1930-2022:
Excel-arket med tilskuerudviklingen kan downloades her.
Konstruktion af xy-plot i WordMat
Vi ønsker at få et overblik over udviklingen. Vi åbner Excel-filen med tilskuerudviklingen, rammer de to sidste kolonner ind og copy paster over i WordMat-arket som vist her:
Indholdet i den grønne boks kaldes et xy-plot og bruges til at visualisere udviklingen. På \(x\)-aksen har vi ”antal af år efter 1930”, og på \(y\)-aksen har vi tilskuertallet. For at gøre det tydeligt går vi ind og ændre aksetitlerne
(bare ved at dobbeltklikke på ”x” og ’y” på akserne):
Flot ser det ud!
Øvelse 3.5.2
Det er nu din tur
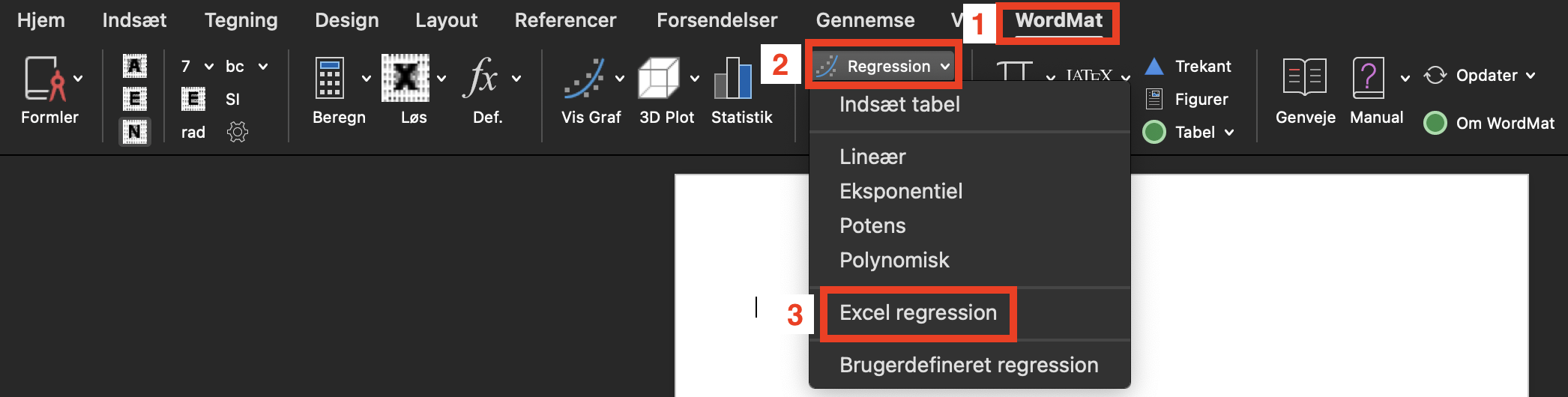
Konstruktion af regressionsmodel i WordMat
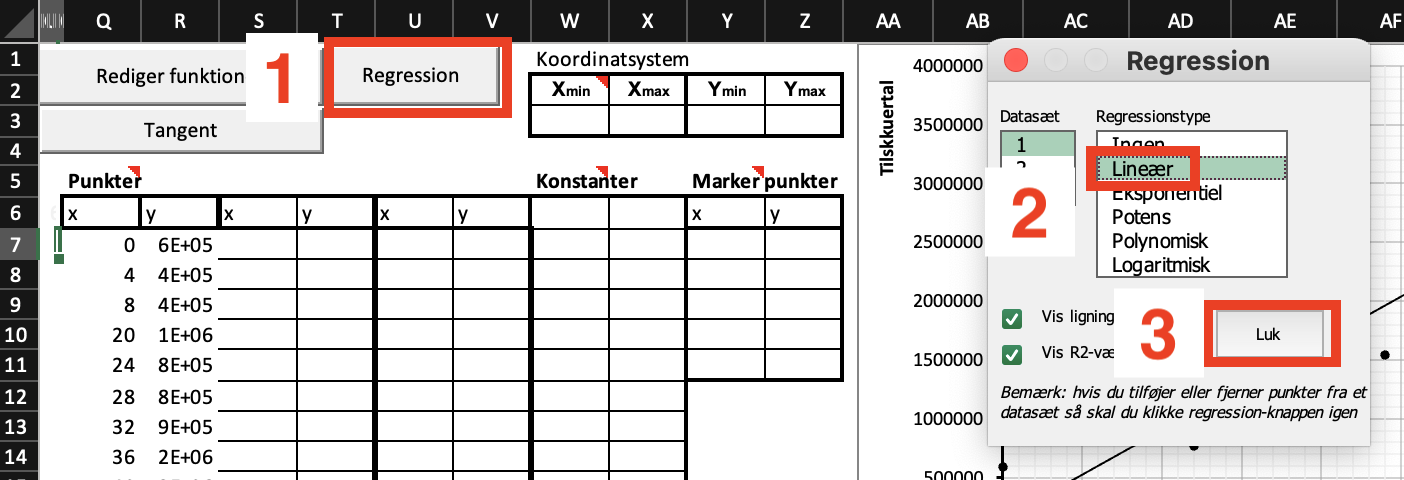
Vi kan se i xy-plottet, at der er en lineær tendens i udviklingen. Dvs. det ser ud som om, at udviklingen følger en lineær funktion, men med nogle tilfældige afvigelser undervejs. Vi kan finde den lineær funktion ved at klikke som
vist her:
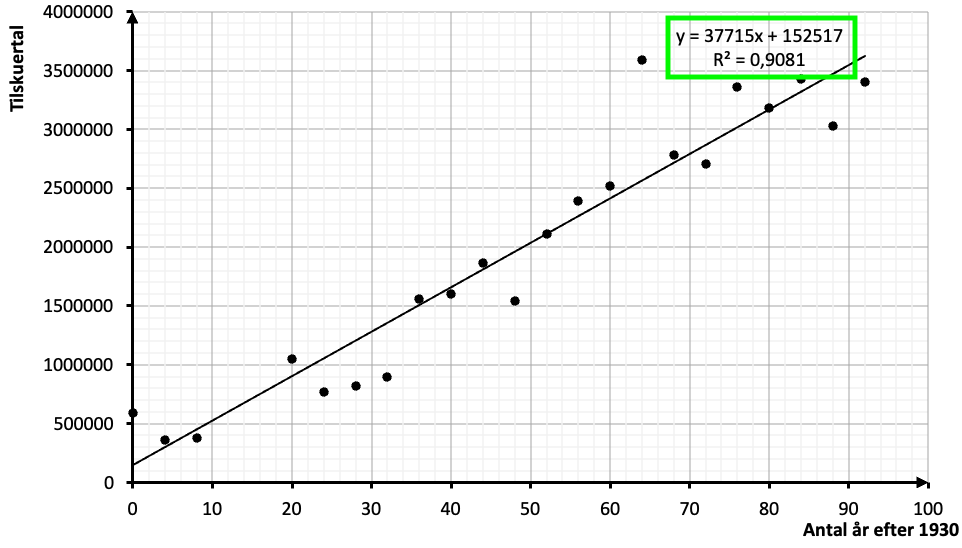
Det giver os:
Vi har nu fundet den linje, som passer bedst muligt til punkterne. Vi ser, at punkterne ligger tilfældigt omkring linjen, og det er godt. Er der systematiske afvigelser fra linjen, er der nemlig noget, der tyder på, at vi ikke kan
beskrive udviklingen med en lineær funktion. I denne grønne boks ses forskriften for linjen:
\[y=37715x+152517\]
Denne funktion kaldes for en lineær model for udviklingen. De \(37715\) kan fortolkes som den årlige stigning af tilskuere i perioden 1930-2022. Det er klart at den faktiske stigning har været
forskellig fra år til år, så de \(37715\) fungerer som et slags ”gennemsnit”. De \(152517\) er tilskuerantallet i år 1930 ifølge modellen. Det faktiske antal tilskuere i 1930 var \(590549\), som det ses i tabellen, så modellen rammer
ret skævt her. I screenshottet ses også at \(=0{,}9081\). Betydningen af dette vil blive forklaret om lidt.
-
Eksempel 3.5.1
Vi kan bruge modellen til at forudsige, hvor mange tilskuere der vil være til VM i 2034. Vi regner først, hvor mange år det er efter 1930:
\[2034-1930=104\]
Vi kan så sætte \(104\) ind i stedet for \(x\) i vores model og få tilskuertallet:
\[y=37715 \cdot 104+152517 = 4074877\]
Så der vil være ca. \(4\) mio. tilskuere til VM i 2034, hvis den nuværende tendens fortsætter.
Øvelse 3.5.3
Du skal nu se om du kan komme til den samme model som mig.
-
a) Opstil en lineær model for udviklingen i antallet af tilskuere i perioden 1930-2022.
-
b) Bestem den årlige vækst i antallet af tilskuere i perioden.
-
c) Hvor mange tilskuere var der, ifølge modellen, til VM i Italien i 1990? Sammenlig med det faktiske antal.
Løsning 3.5.3
-
a) \(y=37715x+152517\)
-
b) Der har været en stigning på \(37715\) tilskuere om året.
-
c) Ifølge modellen var der \(2{,}4\) mio. tilskuere. Det faktiske antal var \(2{,}5\), så det var rimelig godt ramt.
Determinationskoefficient og korrelationskoefficient
Da vi lavede den lineære model for tilskuerudviklingen, fik vi også at vide, at \(R^2=0{,}9081\). Tallet \(R^2\) kaldes determinationskoefficienten er et mål for, hvor godt modellen beskriver udviklingen.
Determinationskoefficienten ligger altid mellem \(0\) og \(1\), og den er tæt på \(1\), når modellen passer godt med udviklingen.
Her er tre eksempler på xy-plot med forskellig \(R^2\) værdi:

\(R^2=1\)

\(R^2=0{,}9\)

\(R^2=0\)
I det første plot er \(R^2=1\), hvilket betyder at alle punkterne ligger på regressionslinjen. Dvs., at modellen giver en fuldstændig beskrivelse af udviklingen. I det andet plot er \(R^2=0{,}9\). Her der en klar voksende lineær
tendens, men punkterne afviger noget fra linjen. I det sidste plot er \(R^2=0\), hvilket umiddelbart er overraskende, da punkter ligger ca. ligeså tæt på linjen som i plot nr. 2. Når vi siger, at \(R^2\) viser, hvor godt modellen
beskriver udviklingen, mener vi i forhold til en vandret linje. I det sidste plot, kan vi ikke finde en lineær funktion, som beskriver udviklingen bedre end en vandret linje, og derfor er \(R^2=0\).
I stedet for at angive determinationskoefficienten, kan man angive en størrelse som hedder korrelationskoefficienten. Den betegnes med \(r\) og fås ved at tage kvadratroden af \(R^2\). Dog skal man sætte et minus på,
hvis udviklingen er aftagende.
Man kunne tro, at hvis bare \(R^2\) er tæt på \(1\), så har man også en god model for ens data. Men sådan er det ikke nødvendigvis. Det er vigtigt, at punkterne ligger på en tilfældig måde omkring linjen, så det rent faktisk ligner
en lineær funktion med nogle tilfældige afvigelser.
-
Eksempel 3.5.2
Betragt xy-plottet:
Den ligner ikke en linje, men lad os alligevel prøve at lave en lineær model:
Denne model har \(R^2=0{,}93\), hvilket da er rimelig tæt på \(1\), men igen, det er tydeligt, at der ikke er tale om en lineær udvikling. Så en høj \(R^2\) er ikke nok til at sikre at man har fat i en god model!
I praksis kan det være svært at afgøre, om der er tale om tilfældige eller systematiske afvigelser alene ud fra xy-plottet og modellen. Nogle gange kan det hjælpe at lave et såkaldt residualplot.
Det er et diagram, som viser afvigelserne mellem punkter og model. WordMat-arket forærer os residualplottet samtidig med at vi laver den lineære model. Det dukker op lige under xy-plottet. Residualplottet for tilskuerudviklingen
til VM i fodbold ser således ud:
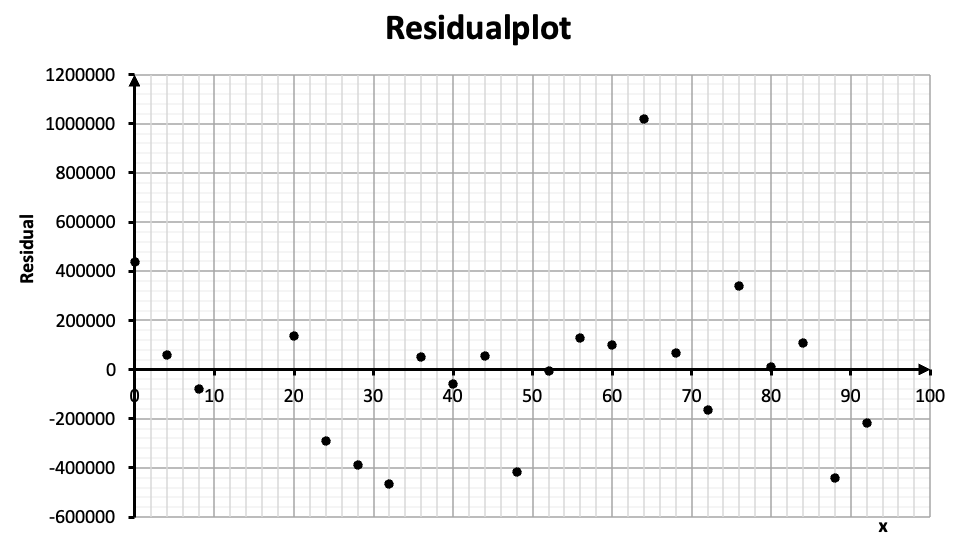
På residualplottet kan vi se, hvordan modellen afviger fra data. F.eks. har det første punkt i residualplottet en \(y\)-værdi på ca \(440.000\). Det betyder at det første punkt i xy-plottet ligger \(440.000\) over linjen. Dvs., at hvis
vi bruger vores model til at regne tilskuertallet for først VM, vil vi få et resultat, der er \(440.000\) for lavt. Vi kalder værdierne i residualplottet for residualer. Residualerne i det konkrete
residualplot ser ud til at fordele sig tilfældigt omkring \(x\)-aksen, så vi har ikke nogen grund til at tro, at der skulle være noget galt med vores model.
Øvelse 3.5.4
Antag at en aftagende lineær model har \(R^2=0{,}9814\)
Løsning 3.5.4
-
a) Vi ser at \(R^2\) er høj, men det betyder ikke at punkterne beskrives godt med en lineær funktion. Vi har brug for et residualplot for at afgøre, om der
er system i residualerne
-
b) \(r=-0{,}99\). Har du husket minusset?
-
Eksempel 3.5.3
Vi vender tilbage til situationen i eksempel 3.5.2:
Som vi også bemærkede i eksempel 3.5.2, kan vi se, at tendensen i punkterne ikke er lineær, og derfor er den lineære model ikke nogen god
model. Laver man et residualplot, vil det se således ud:
Her ses det tydeligt, at residualerne ikke fordeler sig tilfældigt omkring linjen, hvilket altså bekræfter, at vores model er problematisk. Kigger man grundigt på xy-plottet og residualplottet, er det klart, at der ikke er nogen ny
information i residualplottet. I begge diagrammer kan man se, hvordan punkterne afviger fra linjen — det er bare lidt nemmere at se i residualplottet.
Vi vil møde situationer, hvor der er system i residualerne — især når vi kigger på udviklinger over tid. Er der system i residualerne, er det enten fordi modellen er skrupforkert, eller fordi modellen kun formår at beskrive i
udviklingen i grove træk. Vi vil bruge xy-plottet til at afgøre, om det er det er det ene eller det andet. Ser xy-plottet fint ud (tydelig lineær tendens) samtidig med at residualplottet viser system i residualerne vil vi acceptere
modellen, men tage forbehold for, at der er tendenser som modellen ikke fanger. Det skal dog siges, at det er forsimplet statistik vi laver her på HHX, og at man i virkeligheden har forskellige muligheder for at forbedre/ændre
modellen, så man kan slippe af med de systematiske afvigelser.
Øvelse 3.5.5
I denne øvelse skal du se på jordens befolkningstal i perioden 1970-2021.
-
a) Download et Excel-ark med data her og tilføj en søjle til arket, som
indeholder antallet af år efter 1970.
-
b) Opstil et xy-plot, som viser jordens befolkningstal som funktion af antallet af år efter 1970. Vær opmærksom på, at du muligvis skal
højreklikke og vælge ”Indsæt speciel -> Værdier”, når du indsætter dine data i WordMat (det afhænger af, hvordan du har tilføjet den ekstra søjle i det oprindelig ark).
-
c) Opstil en lineær model for udviklingen i befolkningstal og bestem \(R^2\).
-
d) Forklar betydningen af tallene i modellen,
-
e) Bestem hvornår vi, ifølge modellen, er 10 mia. mennesker på jorden.
-
f) Lav et residualplot og vurder modellen.
Løsning 3.5.5
-
a)
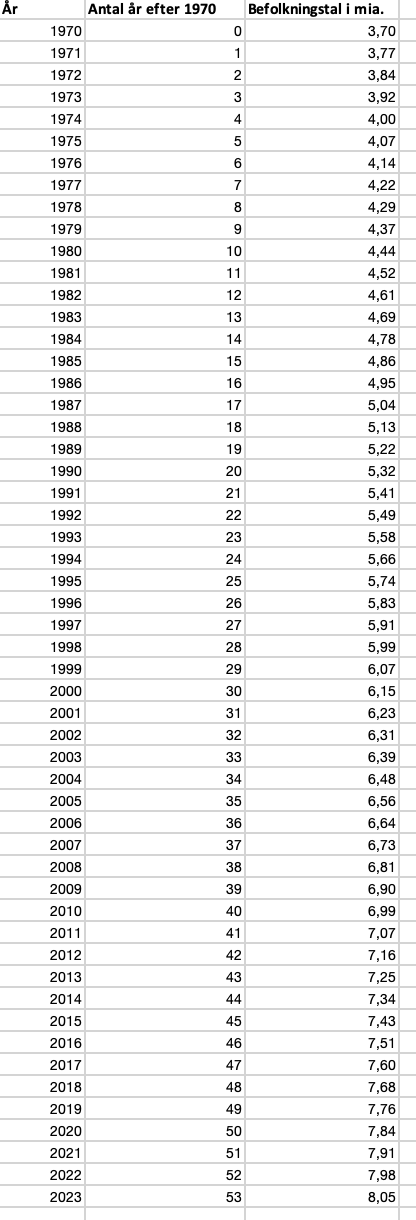
-
b) Har du husket aksetitler?
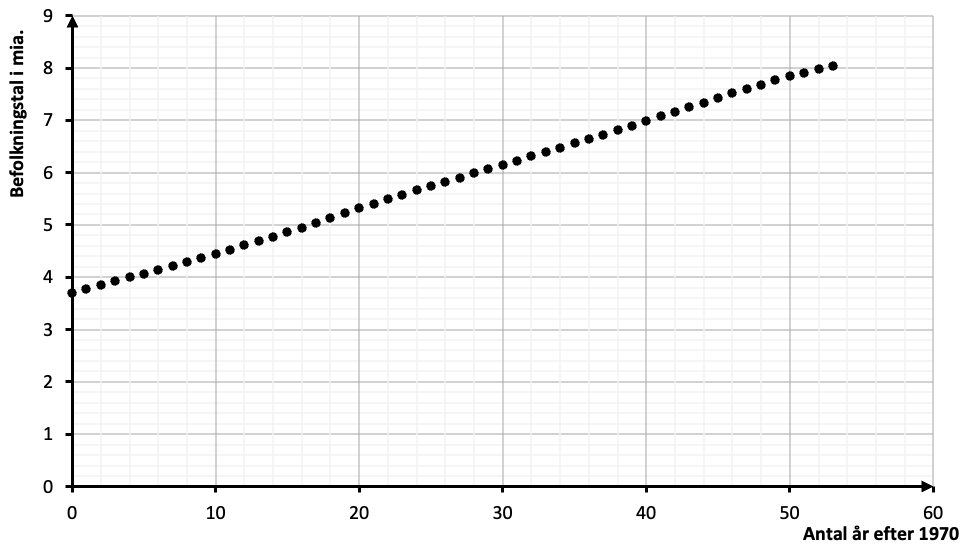
-
c) Modellen er \(y=0{,}0838x+3{,}6376\), hvor \(y\) er befolkningstallet i mia. og \(x\) er antal år efter 2019. Vi har \(R^2=0{,}9997\).
-
d) Tallet \(0{,}0838\) betyder, at der har været en stigning på \(0{,}0838\) mia. mennesker om året. Dvs. at der hvert år kommer \(84\) mio.
mennesker mere på jorden. De \(3{,}6376\) betyder at der var \(3{,}6\) mia. mennesker på jorden i 1970 ifølge modellen.
-
e) År 2046.
-
f)

Vi ser en tydelig lineær tendens i xy-plottet og \(R^2\) er høj. MEN... residualplottet viser, at der er system i residualerne åh nej! Så modellen er ikke helt så god, som det umiddelbart kunne se ud til. Sikke noget møg. Der er altså
tendenser i udviklingen modellen ikke fanger.
Det er vigtigt at bemærke, at den type modeller, vi kigger på her, har en begrænset levetid. Det kan godt være, at der har været en lineær vækst i jordens befolkning de sidste 50 år, men det betyder ikke at væksten også vil være
lineær de næste 50 år. Derfor bør man være forsigtig med at bruge den slags modeller til at fremskrive udviklinger.
Ekstra
Vi skal nu se, hvordan den lineære model fremkommer når man laver regression i WordMat (eller andre tilsvarende værktøjer). Vi tager udgangspunkt i et simpelt xy-plot med kun tre punkter:
Vi tegner nu (bare så godt vi kan) en lineær funktion, der bedst muligt går igennem punkterne. Det er svært, da der er ikke er en tydelige lineær tendens.
Vi markerer nu residualerne:
Residualerne viser afvigelsen mellem model og data for det pågældende punkt. Man kunne godt tro, at det gik ud på at minimere denne afstand. Altså at vi justerede linjen indtil, at den samlede lodrette afstand fra punkterne til
linjen var mindst muligt. Men det er ikke helt det vi gør. I stedet tegner vi kvadrater med residualerne som sidelængder:
Det er arealet af disse kvadrater som WordMat minimerer, når vi laver lineær regression. Altså WordMat finder regressionsmodellen ved at justere på linjen, indtil det samlede areal af kvadraterne ikke kan blive mindre.