MATHHX B
\(\newcommand{\footnotename}{footnote}\)
\(\def \LWRfootnote {1}\)
\(\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#1}}}\)
\(\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}\)
\(\let \LWRorighspace \hspace \)
\(\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }\)
\(\newcommand {\mathnormal }[1]{{#1}}\)
\(\newcommand \ensuremath [1]{#1}\)
\(\newcommand {\LWRframebox }[2][]{\fbox {#2}} \newcommand {\framebox }[1][]{\LWRframebox } \)
\(\newcommand {\setlength }[2]{}\)
\(\newcommand {\addtolength }[2]{}\)
\(\newcommand {\setcounter }[2]{}\)
\(\newcommand {\addtocounter }[2]{}\)
\(\newcommand {\arabic }[1]{}\)
\(\newcommand {\number }[1]{}\)
\(\newcommand {\noalign }[1]{\text {#1}\notag \\}\)
\(\newcommand {\cline }[1]{}\)
\(\newcommand {\directlua }[1]{\text {(directlua)}}\)
\(\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}\)
\(\newcommand {\protect }{}\)
\(\def \LWRabsorbnumber #1 {}\)
\(\def \LWRabsorbquotenumber "#1 {}\)
\(\newcommand {\LWRabsorboption }[1][]{}\)
\(\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }\)
\(\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }\)
\(\def \mathcode #1={\mathchar }\)
\(\let \delcode \mathcode \)
\(\let \delimiter \mathchar \)
\(\def \oe {\unicode {x0153}}\)
\(\def \OE {\unicode {x0152}}\)
\(\def \ae {\unicode {x00E6}}\)
\(\def \AE {\unicode {x00C6}}\)
\(\def \aa {\unicode {x00E5}}\)
\(\def \AA {\unicode {x00C5}}\)
\(\def \o {\unicode {x00F8}}\)
\(\def \O {\unicode {x00D8}}\)
\(\def \l {\unicode {x0142}}\)
\(\def \L {\unicode {x0141}}\)
\(\def \ss {\unicode {x00DF}}\)
\(\def \SS {\unicode {x1E9E}}\)
\(\def \dag {\unicode {x2020}}\)
\(\def \ddag {\unicode {x2021}}\)
\(\def \P {\unicode {x00B6}}\)
\(\def \copyright {\unicode {x00A9}}\)
\(\def \pounds {\unicode {x00A3}}\)
\(\let \LWRref \ref \)
\(\renewcommand {\ref }{\ifstar \LWRref \LWRref }\)
\( \newcommand {\multicolumn }[3]{#3}\)
\(\require {textcomp}\)
\(\require {colortbl}\)
\(\let \LWRorigcolumncolor \columncolor \)
\(\renewcommand {\columncolor }[2][named]{\LWRorigcolumncolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\let \LWRorigrowcolor \rowcolor \)
\(\renewcommand {\rowcolor }[2][named]{\LWRorigrowcolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\let \LWRorigcellcolor \cellcolor \)
\(\renewcommand {\cellcolor }[2][named]{\LWRorigcellcolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\newcommand {\tothe }[1]{^{#1}}\)
\(\newcommand {\raiseto }[2]{{#2}^{#1}}\)
\(\newcommand {\LWRsiunitxEND }{}\)
\(\def \LWRsiunitxang #1;#2;#3;#4\LWRsiunitxEND {\ifblank {#1}{}{\num {#1}\degree }\ifblank {#2}{}{\num {#2}^{\unicode {x2032}}}\ifblank {#3}{}{\num {#3}^{\unicode {x2033}}}}\)
\(\newcommand {\ang }[2][]{\LWRsiunitxang #2;;;\LWRsiunitxEND }\)
\(\def \LWRsiunitxdistribunit {}\)
\(\newcommand {\LWRsiunitxENDTWO }{}\)
\(\def \LWRsiunitxprintdecimalsubtwo #1,#2,#3\LWRsiunitxENDTWO {\ifblank {#1}{0}{\mathrm {#1}}\ifblank {#2}{}{{\LWRsiunitxdecimal }\mathrm {#2}}}\)
\(\def \LWRsiunitxprintdecimalsub #1.#2.#3\LWRsiunitxEND {\LWRsiunitxprintdecimalsubtwo #1,,\LWRsiunitxENDTWO \ifblank {#2}{}{{\LWRsiunitxdecimal }\LWRsiunitxprintdecimalsubtwo
#2,,\LWRsiunitxENDTWO }}\)
\(\newcommand {\LWRsiunitxprintdecimal }[1]{\LWRsiunitxprintdecimalsub #1...\LWRsiunitxEND }\)
\(\def \LWRsiunitxnumplus #1+#2+#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxprintdecimal {#1}}{\ifblank {#1}{\LWRsiunitxprintdecimal {#2}}{\LWRsiunitxprintdecimal {#1}\unicode
{x02B}\LWRsiunitxprintdecimal {#2}}}\LWRsiunitxdistribunit }\)
\(\def \LWRsiunitxnumminus #1-#2-#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumplus #1+++\LWRsiunitxEND }{\ifblank {#1}{}{\LWRsiunitxprintdecimal {#1}}\unicode {x02212}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\def \LWRsiunitxnumpmmacro #1\pm #2\pm #3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumminus #1---\LWRsiunitxEND }{\LWRsiunitxprintdecimal {#1}\unicode {x0B1}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\def \LWRsiunitxnumpm #1+-#2+-#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumpmmacro #1\pm \pm \pm \LWRsiunitxEND }{\LWRsiunitxprintdecimal {#1}\unicode {x0B1}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\newcommand {\LWRsiunitxnumscientific }[2]{\ifblank {#1}{}{\ifstrequal {#1}{-}{-}{\LWRsiunitxprintdecimal {#1}\times }}10^{\LWRsiunitxprintdecimal {#2}}\LWRsiunitxdistribunit }\)
\(\def \LWRsiunitxnumD #1D#2D#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumpm #1+-+-\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumd #1d#2d#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumD #1DDD\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumE #1E#2E#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumd #1ddd\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnume #1e#2e#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumE #1EEE\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumx #1x#2x#3x#4\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnume #1eee\LWRsiunitxEND }{\ifblank {#3}{\LWRsiunitxnume #1eee\LWRsiunitxEND \times \LWRsiunitxnume
#2eee\LWRsiunitxEND }{\LWRsiunitxnume #1eee\LWRsiunitxEND \times \LWRsiunitxnume #2eee\LWRsiunitxEND \times \LWRsiunitxnume #3eee\LWRsiunitxEND }}}\)
\(\newcommand {\num }[2][]{\LWRsiunitxnumx #2xxxxx\LWRsiunitxEND }\)
\(\newcommand {\si }[2][]{\mathrm {\gsubstitute {#2}{~}{\,}}}\)
\(\def \LWRsiunitxSIopt #1[#2]#3{\def \LWRsiunitxdistribunit {\,\si {#3}}{#2}\num {#1}\def \LWRsiunitxdistribunit {}}\)
\(\newcommand {\LWRsiunitxSI }[2]{\def \LWRsiunitxdistribunit {\,\si {#2}}\num {#1}\def \LWRsiunitxdistribunit {}}\)
\(\newcommand {\SI }[2][]{\ifnextchar [{\LWRsiunitxSIopt {#2}}{\LWRsiunitxSI {#2}}}\)
\(\newcommand {\numlist }[2][]{\text {#2}}\)
\(\newcommand {\numrange }[3][]{\num {#2}\ \LWRsiunitxrangephrase \ \num {#3}}\)
\(\newcommand {\SIlist }[3][]{\text {#2}\,\si {#3}}\)
\(\newcommand {\SIrange }[4][]{\num {#2}\,#4\ \LWRsiunitxrangephrase \ \num {#3}\,#4}\)
\(\newcommand {\tablenum }[2][]{\mathrm {#2}}\)
\(\newcommand {\ampere }{\mathrm {A}}\)
\(\newcommand {\candela }{\mathrm {cd}}\)
\(\newcommand {\kelvin }{\mathrm {K}}\)
\(\newcommand {\kilogram }{\mathrm {kg}}\)
\(\newcommand {\metre }{\mathrm {m}}\)
\(\newcommand {\mole }{\mathrm {mol}}\)
\(\newcommand {\second }{\mathrm {s}}\)
\(\newcommand {\becquerel }{\mathrm {Bq}}\)
\(\newcommand {\degreeCelsius }{\unicode {x2103}}\)
\(\newcommand {\coulomb }{\mathrm {C}}\)
\(\newcommand {\farad }{\mathrm {F}}\)
\(\newcommand {\gray }{\mathrm {Gy}}\)
\(\newcommand {\hertz }{\mathrm {Hz}}\)
\(\newcommand {\henry }{\mathrm {H}}\)
\(\newcommand {\joule }{\mathrm {J}}\)
\(\newcommand {\katal }{\mathrm {kat}}\)
\(\newcommand {\lumen }{\mathrm {lm}}\)
\(\newcommand {\lux }{\mathrm {lx}}\)
\(\newcommand {\newton }{\mathrm {N}}\)
\(\newcommand {\ohm }{\mathrm {\Omega }}\)
\(\newcommand {\pascal }{\mathrm {Pa}}\)
\(\newcommand {\radian }{\mathrm {rad}}\)
\(\newcommand {\siemens }{\mathrm {S}}\)
\(\newcommand {\sievert }{\mathrm {Sv}}\)
\(\newcommand {\steradian }{\mathrm {sr}}\)
\(\newcommand {\tesla }{\mathrm {T}}\)
\(\newcommand {\volt }{\mathrm {V}}\)
\(\newcommand {\watt }{\mathrm {W}}\)
\(\newcommand {\weber }{\mathrm {Wb}}\)
\(\newcommand {\day }{\mathrm {d}}\)
\(\newcommand {\degree }{\mathrm {^\circ }}\)
\(\newcommand {\hectare }{\mathrm {ha}}\)
\(\newcommand {\hour }{\mathrm {h}}\)
\(\newcommand {\litre }{\mathrm {l}}\)
\(\newcommand {\liter }{\mathrm {L}}\)
\(\newcommand {\arcminute }{^\prime }\)
\(\newcommand {\minute }{\mathrm {min}}\)
\(\newcommand {\arcsecond }{^{\prime \prime }}\)
\(\newcommand {\tonne }{\mathrm {t}}\)
\(\newcommand {\astronomicalunit }{au}\)
\(\newcommand {\atomicmassunit }{u}\)
\(\newcommand {\bohr }{\mathit {a}_0}\)
\(\newcommand {\clight }{\mathit {c}_0}\)
\(\newcommand {\dalton }{\mathrm {D}_\mathrm {a}}\)
\(\newcommand {\electronmass }{\mathit {m}_{\mathrm {e}}}\)
\(\newcommand {\electronvolt }{\mathrm {eV}}\)
\(\newcommand {\elementarycharge }{\mathit {e}}\)
\(\newcommand {\hartree }{\mathit {E}_{\mathrm {h}}}\)
\(\newcommand {\planckbar }{\mathit {\unicode {x210F}}}\)
\(\newcommand {\angstrom }{\mathrm {\unicode {x212B}}}\)
\(\let \LWRorigbar \bar \)
\(\newcommand {\barn }{\mathrm {b}}\)
\(\newcommand {\bel }{\mathrm {B}}\)
\(\newcommand {\decibel }{\mathrm {dB}}\)
\(\newcommand {\knot }{\mathrm {kn}}\)
\(\newcommand {\mmHg }{\mathrm {mmHg}}\)
\(\newcommand {\nauticalmile }{\mathrm {M}}\)
\(\newcommand {\neper }{\mathrm {Np}}\)
\(\newcommand {\yocto }{\mathrm {y}}\)
\(\newcommand {\zepto }{\mathrm {z}}\)
\(\newcommand {\atto }{\mathrm {a}}\)
\(\newcommand {\femto }{\mathrm {f}}\)
\(\newcommand {\pico }{\mathrm {p}}\)
\(\newcommand {\nano }{\mathrm {n}}\)
\(\newcommand {\micro }{\mathrm {\unicode {x00B5}}}\)
\(\newcommand {\milli }{\mathrm {m}}\)
\(\newcommand {\centi }{\mathrm {c}}\)
\(\newcommand {\deci }{\mathrm {d}}\)
\(\newcommand {\deca }{\mathrm {da}}\)
\(\newcommand {\hecto }{\mathrm {h}}\)
\(\newcommand {\kilo }{\mathrm {k}}\)
\(\newcommand {\mega }{\mathrm {M}}\)
\(\newcommand {\giga }{\mathrm {G}}\)
\(\newcommand {\tera }{\mathrm {T}}\)
\(\newcommand {\peta }{\mathrm {P}}\)
\(\newcommand {\exa }{\mathrm {E}}\)
\(\newcommand {\zetta }{\mathrm {Z}}\)
\(\newcommand {\yotta }{\mathrm {Y}}\)
\(\newcommand {\percent }{\mathrm {\%}}\)
\(\newcommand {\meter }{\mathrm {m}}\)
\(\newcommand {\metre }{\mathrm {m}}\)
\(\newcommand {\gram }{\mathrm {g}}\)
\(\newcommand {\kg }{\kilo \gram }\)
\(\newcommand {\of }[1]{_{\mathrm {#1}}}\)
\(\newcommand {\squared }{^2}\)
\(\newcommand {\square }[1]{\mathrm {#1}^2}\)
\(\newcommand {\cubed }{^3}\)
\(\newcommand {\cubic }[1]{\mathrm {#1}^3}\)
\(\newcommand {\per }{\,\mathrm {/}}\)
\(\newcommand {\celsius }{\unicode {x2103}}\)
\(\newcommand {\fg }{\femto \gram }\)
\(\newcommand {\pg }{\pico \gram }\)
\(\newcommand {\ng }{\nano \gram }\)
\(\newcommand {\ug }{\micro \gram }\)
\(\newcommand {\mg }{\milli \gram }\)
\(\newcommand {\g }{\gram }\)
\(\newcommand {\kg }{\kilo \gram }\)
\(\newcommand {\amu }{\mathrm {u}}\)
\(\newcommand {\nm }{\nano \metre }\)
\(\newcommand {\um }{\micro \metre }\)
\(\newcommand {\mm }{\milli \metre }\)
\(\newcommand {\cm }{\centi \metre }\)
\(\newcommand {\dm }{\deci \metre }\)
\(\newcommand {\m }{\metre }\)
\(\newcommand {\km }{\kilo \metre }\)
\(\newcommand {\as }{\atto \second }\)
\(\newcommand {\fs }{\femto \second }\)
\(\newcommand {\ps }{\pico \second }\)
\(\newcommand {\ns }{\nano \second }\)
\(\newcommand {\us }{\micro \second }\)
\(\newcommand {\ms }{\milli \second }\)
\(\newcommand {\s }{\second }\)
\(\newcommand {\fmol }{\femto \mol }\)
\(\newcommand {\pmol }{\pico \mol }\)
\(\newcommand {\nmol }{\nano \mol }\)
\(\newcommand {\umol }{\micro \mol }\)
\(\newcommand {\mmol }{\milli \mol }\)
\(\newcommand {\mol }{\mol }\)
\(\newcommand {\kmol }{\kilo \mol }\)
\(\newcommand {\pA }{\pico \ampere }\)
\(\newcommand {\nA }{\nano \ampere }\)
\(\newcommand {\uA }{\micro \ampere }\)
\(\newcommand {\mA }{\milli \ampere }\)
\(\newcommand {\A }{\ampere }\)
\(\newcommand {\kA }{\kilo \ampere }\)
\(\newcommand {\ul }{\micro \litre }\)
\(\newcommand {\ml }{\milli \litre }\)
\(\newcommand {\l }{\litre }\)
\(\newcommand {\hl }{\hecto \litre }\)
\(\newcommand {\uL }{\micro \liter }\)
\(\newcommand {\mL }{\milli \liter }\)
\(\newcommand {\L }{\liter }\)
\(\newcommand {\hL }{\hecto \liter }\)
\(\newcommand {\mHz }{\milli \hertz }\)
\(\newcommand {\Hz }{\hertz }\)
\(\newcommand {\kHz }{\kilo \hertz }\)
\(\newcommand {\MHz }{\mega \hertz }\)
\(\newcommand {\GHz }{\giga \hertz }\)
\(\newcommand {\THz }{\tera \hertz }\)
\(\newcommand {\mN }{\milli \newton }\)
\(\newcommand {\N }{\newton }\)
\(\newcommand {\kN }{\kilo \newton }\)
\(\newcommand {\MN }{\mega \newton }\)
\(\newcommand {\Pa }{\pascal }\)
\(\newcommand {\kPa }{\kilo \pascal }\)
\(\newcommand {\MPa }{\mega \pascal }\)
\(\newcommand {\GPa }{\giga \pascal }\)
\(\newcommand {\mohm }{\milli \ohm }\)
\(\newcommand {\kohm }{\kilo \ohm }\)
\(\newcommand {\Mohm }{\mega \ohm }\)
\(\newcommand {\pV }{\pico \volt }\)
\(\newcommand {\nV }{\nano \volt }\)
\(\newcommand {\uV }{\micro \volt }\)
\(\newcommand {\mV }{\milli \volt }\)
\(\newcommand {\V }{\volt }\)
\(\newcommand {\kV }{\kilo \volt }\)
\(\newcommand {\W }{\watt }\)
\(\newcommand {\uW }{\micro \watt }\)
\(\newcommand {\mW }{\milli \watt }\)
\(\newcommand {\kW }{\kilo \watt }\)
\(\newcommand {\MW }{\mega \watt }\)
\(\newcommand {\GW }{\giga \watt }\)
\(\newcommand {\J }{\joule }\)
\(\newcommand {\uJ }{\micro \joule }\)
\(\newcommand {\mJ }{\milli \joule }\)
\(\newcommand {\kJ }{\kilo \joule }\)
\(\newcommand {\eV }{\electronvolt }\)
\(\newcommand {\meV }{\milli \electronvolt }\)
\(\newcommand {\keV }{\kilo \electronvolt }\)
\(\newcommand {\MeV }{\mega \electronvolt }\)
\(\newcommand {\GeV }{\giga \electronvolt }\)
\(\newcommand {\TeV }{\tera \electronvolt }\)
\(\newcommand {\kWh }{\kilo \watt \hour }\)
\(\newcommand {\F }{\farad }\)
\(\newcommand {\fF }{\femto \farad }\)
\(\newcommand {\pF }{\pico \farad }\)
\(\newcommand {\K }{\mathrm {K}}\)
\(\newcommand {\dB }{\mathrm {dB}}\)
\(\newcommand {\kibi }{\mathrm {Ki}}\)
\(\newcommand {\mebi }{\mathrm {Mi}}\)
\(\newcommand {\gibi }{\mathrm {Gi}}\)
\(\newcommand {\tebi }{\mathrm {Ti}}\)
\(\newcommand {\pebi }{\mathrm {Pi}}\)
\(\newcommand {\exbi }{\mathrm {Ei}}\)
\(\newcommand {\zebi }{\mathrm {Zi}}\)
\(\newcommand {\yobi }{\mathrm {Yi}}\)
\(\let \unit \si \)
\(\let \qty \SI \)
\(\let \qtylist \SIlist \)
\(\let \qtyrange \SIrange \)
\(\let \numproduct \num \)
\(\let \qtyproduct \SI \)
\(\let \complexnum \num \)
\(\newcommand {\complexqty }[3][]{(\complexnum {#2})\si {#3}}\)
\(\newcommand {\mleft }{\left }\)
\(\newcommand {\mright }{\right }\)
\(\newcommand {\mleftright }{}\)
\(\newcommand {\mleftrightrestore }{}\)
\(\require {gensymb}\)
\(\newcommand {\intertext }[1]{\text {#1}\notag \\}\)
\(\let \Hat \hat \)
\(\let \Check \check \)
\(\let \Tilde \tilde \)
\(\let \Acute \acute \)
\(\let \Grave \grave \)
\(\let \Dot \dot \)
\(\let \Ddot \ddot \)
\(\let \Breve \breve \)
\(\let \Bar \bar \)
\(\let \Vec \vec \)
\(\require {cancel}\)
\(\newcommand {\Dm }{\operatorname {Dm}}\)
\(\newcommand {\Vm }{\operatorname {Vm}}\)
\(\newcommand {\Var }{\operatorname {Var}}\)
\(\newcommand {\tcbset }[1]{}\)
\(\newcommand {\tcbsetforeverylayer }[1]{}\)
\(\newcommand {\tcbox }[2][]{\boxed {\text {#2}}}\)
\(\newcommand {\tcboxfit }[2][]{\boxed {#2}}\)
\(\newcommand {\tcblower }{}\)
\(\newcommand {\tcbline }{}\)
\(\newcommand {\tcbtitle }{}\)
\(\newcommand {\tcbsubtitle [2][]{\mathrm {#2}}}\)
\(\newcommand {\tcboxmath }[2][]{\boxed {#2}}\)
\(\newcommand {\tcbhighmath }[2][]{\boxed {#2}}\)
\(\newcommand {\toprule }[1][]{\hline }\)
\(\let \midrule \toprule \)
\(\let \bottomrule \toprule \)
\(\def \LWRbooktabscmidruleparen (#1)#2{}\)
\(\newcommand {\LWRbooktabscmidrulenoparen }[1]{}\)
\(\newcommand {\cmidrule }[1][]{\ifnextchar (\LWRbooktabscmidruleparen \LWRbooktabscmidrulenoparen }\)
\(\newcommand {\morecmidrules }{}\)
\(\newcommand {\specialrule }[3]{\hline }\)
\(\newcommand {\addlinespace }[1][]{}\)
\(\def \LWRsiunitxrangephrase { \protect \mbox {to (numerical range)} }\)
\(\def \LWRsiunitxdecimal {.}\)
3.6 Lineær regression i Excel og GeoGebra
OBS: Det afsnit er for elever på den gamle ordning (startet før 2024) eller for elever, som ønsker at lære flere metoder til at lave lineær regression. Er man på den nye ordning er afsnittet valgfrit.
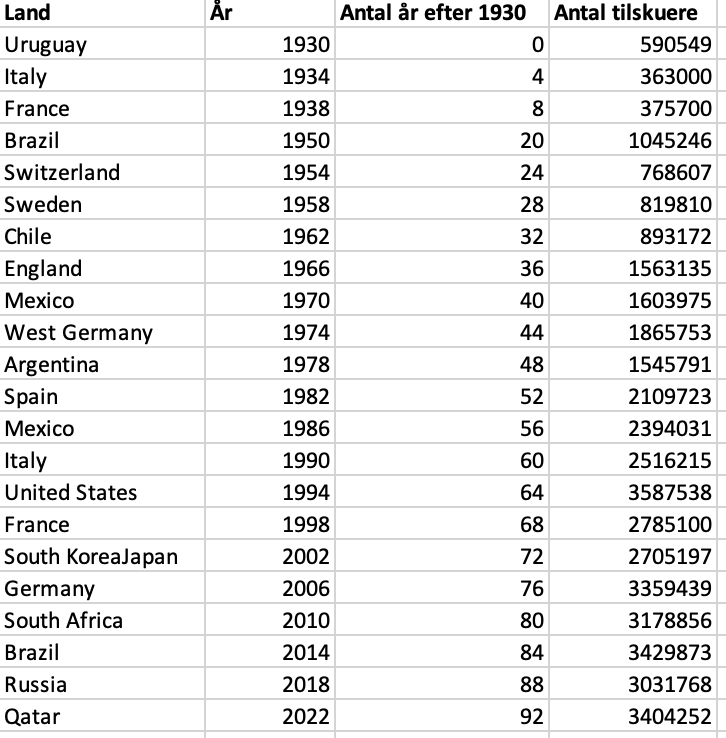
Lineær regression bruges til at beskrive udviklinger, som er tilnærmelsesvist lineære. Vi vil i det følgende kigge på tilskuerudviklingen ved VM i fodbold i perioden 1930-2022. Vi vil tage udgangspunkt i et Excel-ark, der indeholder
følgende:
Konstruktion af xy-plot i Excel
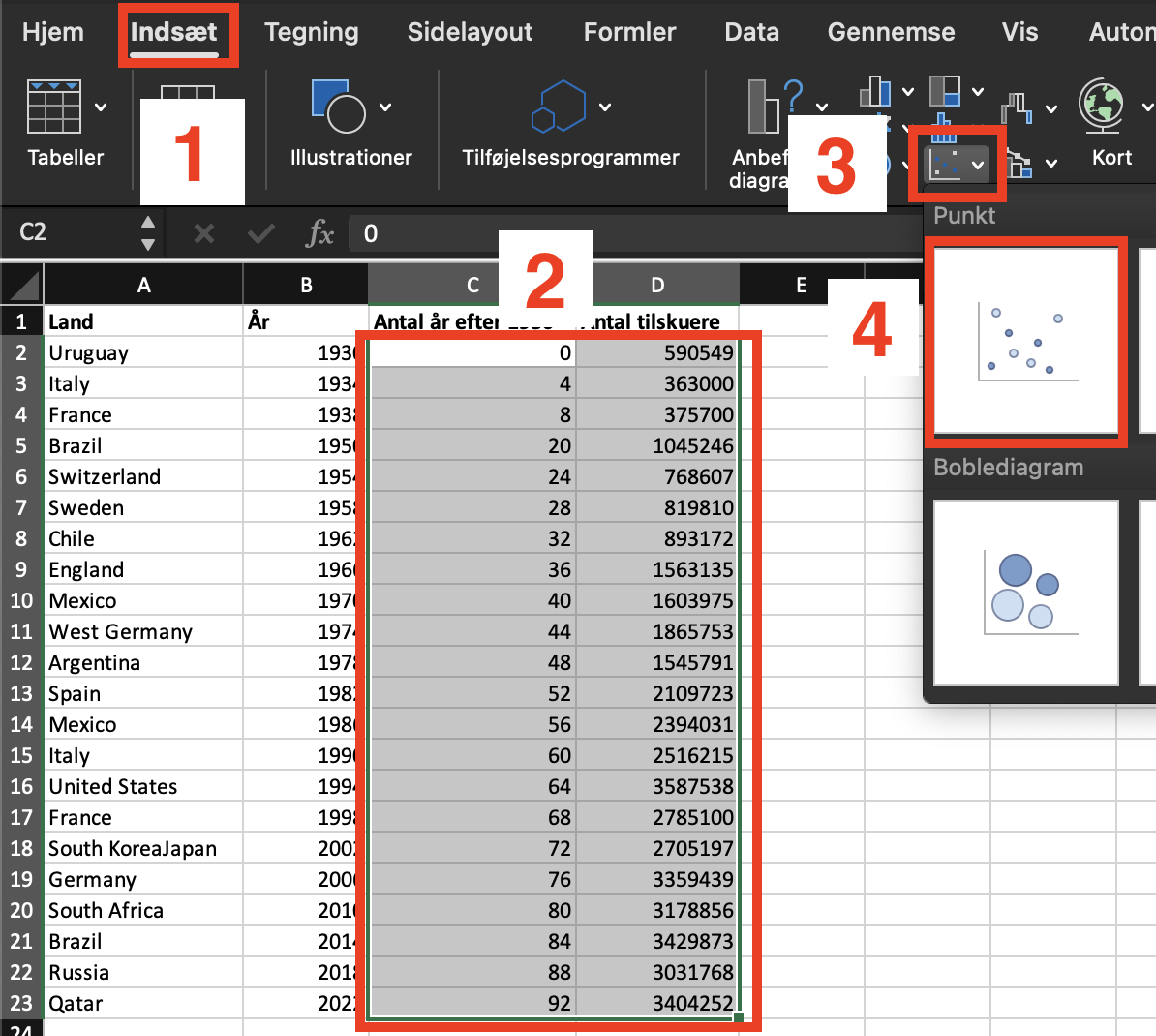
Vi ønsker at få et overblik over udviklingen. Vi åbner Excel-filen, rammer de to sidste kolonner ind og indsætter et punktdiagram:
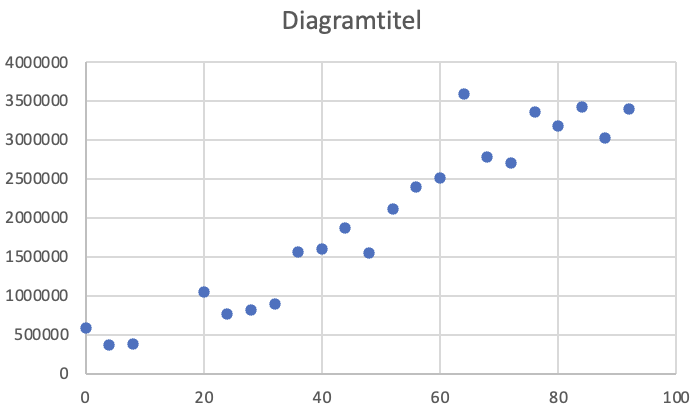
Det giver os følgende diagram:
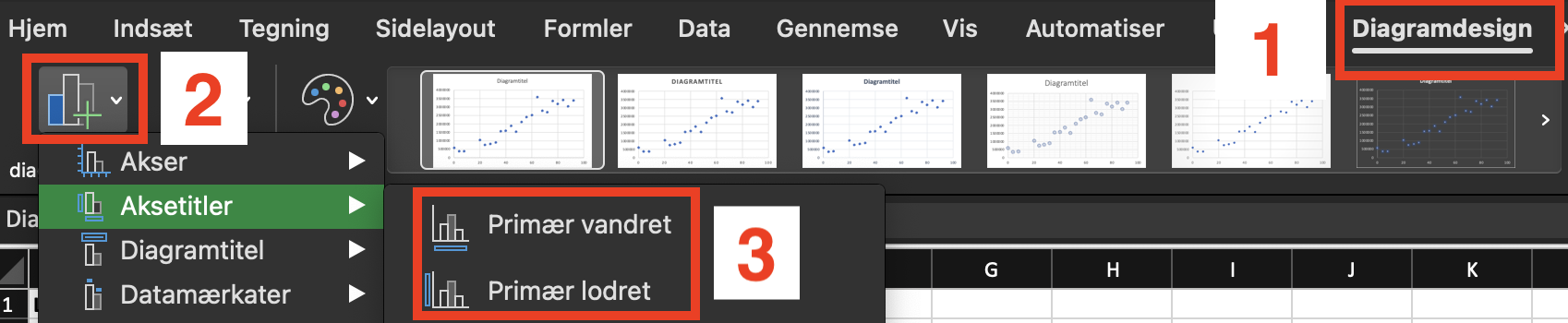
Det er sådan set et fint diagram borset fra, at man ikke kan se, hvad det forstiller. Vi tilføjer aksetitler:
Klikker vi diagramtitlen og aksetitlerne, kan vi ændre dem:
Det var meget bedre. Nu kan man se, hvad diagrammet forstiller. Et sådan diagram kaldes et xy-plot. Vi kan se, at der er en lineær tendens i udviklingen. Dvs. det ser ud som om, at udviklingen følger en lineær funktion,
men med nogle tilfældige udsving undervejs.
Øvelse 3.6.1
Excel-arket med tilskuerudviklingen kan downloades downloades her.
Lineær regression i Excel
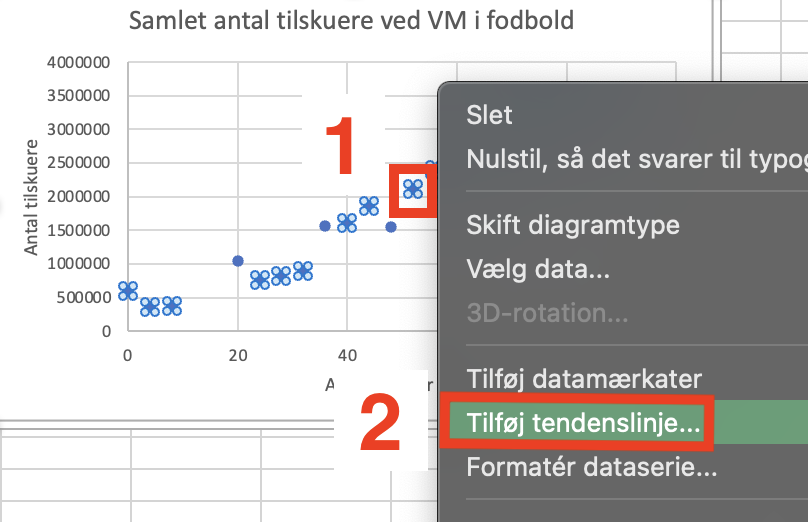
Vi vil nu finde en forskrift for den linje, som passer bedst muligt med punkterne. Vi højreklikker på et af punkterne xy-plottet og tilføjer en tendenslinje:
Ude til højre vælger vi ”Lineær”, ”Vis ligning i diagram” og ”Vis R-kvadreret værdi i diagram”
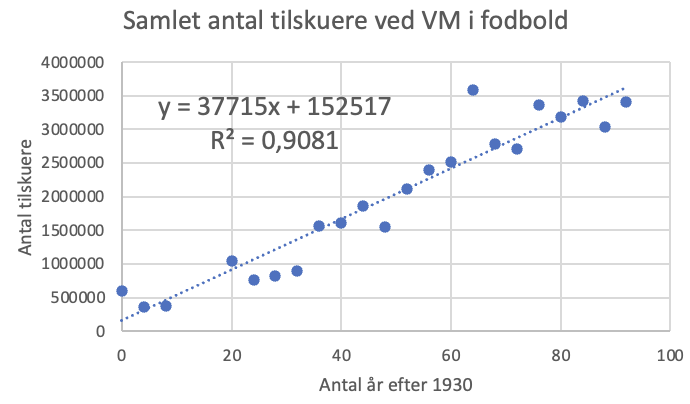
Det giver os følgende:
Excel har nu fundet den linje, som passer bedst muligt til punkterne. Vi ser, at punkterne ligger tilfældigt omkring linjen, og det er godt. Er der systematiske afvigelser fra linjen, er der nemlig noget, der tyder på, at vi ikke kan
beskrive udviklingen med en lineær funktion. Excel har også givet os forskriften for linjen:
\[y=37715x+152517\]
Denne funktion kaldes for en lineær model for udviklingen. De \(37715\) kan fortolkes som den årlige stigning af tilskuere i perioden 1930-2022. Det er klart at den faktiske stigning har været
forskellig fra år til år, så de \(37715\) fungerer som et slags ”gennemsnit”. De \(152517\) er tilskuerantallet i år 1930 ifølge modellen. Det faktiske antal tilskuere i 1930 var \(590549\), som det ses i tabellen, så modellen rammer
ret skævt her. I screenshottet ses også at \(R^2=0{,}91\). Betydningen af dette vil blive forklaret om lidt.
-
Eksempel 3.6.1
Vi kan bruge modellen til at forudsige, hvor mange tilskuere der vil være til VM i 2034. Vi regner først, hvor mange år det er efter 1930:
\[2034-1930=104\]
Vi kan så sætte \(104\) ind i stedet for \(x\) i vores model og få tilskuertallet:
\[y=37715 \cdot 104+152517 = 4074877\]
Så der vil være ca. \(4\) mio. tilskuere til VM i 2034, hvis tendensen fortsætter.
Øvelse 3.6.2
Du skal nu arbejde videre med dit Excel-ark fra sidste øvelse og se, om du kan komme til den samme model som mig.
-
a) Opstil en lineær model for udviklingen i antallet af tilskuere i perioden 1930-2022.
-
b) Bestem den årlige vækst i antallet af tilskuere i perioden.
-
c) Hvor mange tilskuere var der, ifølge modellen, til VM i Italien i 1990? Sammenlig med det faktiske antal.
Løsning 3.6.2
-
a) \(y=37715x+152517\)
-
b) Der har været en stigning på \(37715\) tilskuere om året
-
c) Ifølge modellen var der \(2{,}4\) mio. tilskuere. Det faktiske antal var \(2{,}5\), så det var rimelig godt ramt.
Determinationskoefficient og korrelationskoefficient
Da vi opstillede den lineære model for tilskuerudviklingen, fik vi også at vide, at \(R^2=0{,}91\). Tallet \(R^2\) kaldes determinationskoefficienten er et mål for, hvor godt modellen beskriver udviklingen.
Determinationskoefficienten ligger altid mellem \(0\) og \(1\), og den er tæt på \(1\), når modellen passer godt med udviklingen.
Her er tre eksempler på xy-plot med forskellig \(R^2\) værdi:

\(R^2=1\)

\(R^2=0{,}9\)

\(R^2=0\)
I det første plot er \(R^2=1\), og det er den kun, når punkterne ligger på regressionslinjen. Det betyder, at modellen giver en fuldstændig beskrivelse af udviklingen. I det andet plot er \(R^2=0{,}9\). Her der en klar voksende
lineær tendens, men punkterne varierer noget fra linjen. I det sidste plot er \(R^2=0\), hvilket umiddelbart er overraskende, da punkter ligger ca. ligeså tæt på linjen som i plot nr. 2. Når vi siger, at \(R^2\) viser, hvor godt modellen
beskriver udviklingen, mener vi i forhold til en vandret linje. I det sidste plot, kan vi ikke finde en lineær funktion, som beskriver udviklingen bedre end en vandret linje, og derfor er \(R^2=0\).
Man kunne tro, at hvis bare \(R^2\) er tæt på \(1\), så har man også en god model for ens data. Men sådan er det ikke nødvendigvis. Det er vigtigt, at punkterne ligger på en tilfældig måde omkring linjen, så det rent faktisk ligner
en lineær funktion med nogle tilfældige afvigelser.
-
Eksempel 3.6.2
Betragt xy-plottet:
Den ligner ikke en linje, men lad os alligevel prøve at lave en lineær model:
Denne model har \(R^2=0{,}93\), hvilket da er rimelig tæt på \(1\), men vi kan se at punkterne ikke ligger tilfældigt omkring linjen. Først ligger de over, så er der et langt stykke, hvor de ligger under, og til sidst ligger de over
igen. Så udviklingen kan ikke beskrives med en lineær model.
I stedet for at angive determinationskoefficienten kan man angive en størrelse som hedder korrelationskoefficienten. Den betegnes med \(r\) og fås ved at tage kvadratroden af \(R^2\). Dog skal man sætte et minus på,
hvis udviklingen er aftagende.
Øvelse 3.6.3
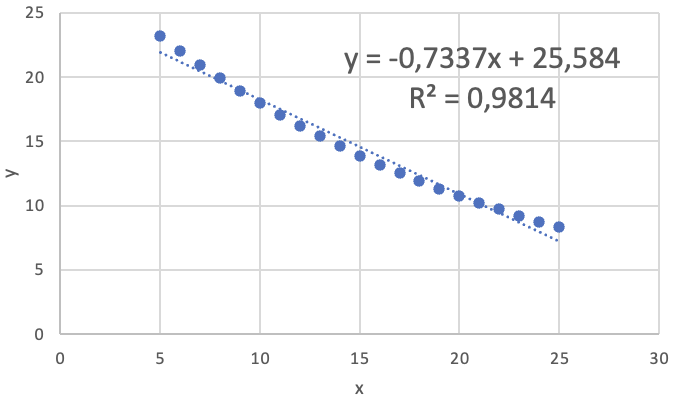
Betragt den følgende xy-plot lavet i Excel:
Løsning 3.6.3
-
a) Vi ser at \(R^2\) er høj, så punkterne ligger tæt på linjen, men udsvingene fra linjen er ikke tilfældige, så vi bør ikke modellere udviklingen med en
lineær model.
-
b) \(r=-0{,}99\). Har du husket minusset?
Hvis du har tænkt dig at lave ekstraafsnittet, så gør det inden du regner den næste øvelse. I ekstraafsnittet får du nemlig et alternativ til at regne i Excel.
Øvelse 3.6.4
I denne øvelse skal vi se på jordens befolkningstal i perioden 1970-2021.
-
a) Downloade data her og tilføj en søjle i Excel, som indeholder antallet af år
efter 1970.
-
b) Opstil et xy-plot, som viser jordens befolkningstal som funktion af antallet af år efter 1970.
-
c) Opstil en lineær model for udviklingen i befolkningstal, og vurder om modellen giver en god beskrivelse af data.
-
d) Forklar betydningen af tallene i modellen,
-
e) Bestem hvornår vi, ifølge modellen, er 10 mia. mennesker på jorden.
Løsning 3.6.4
-
a)
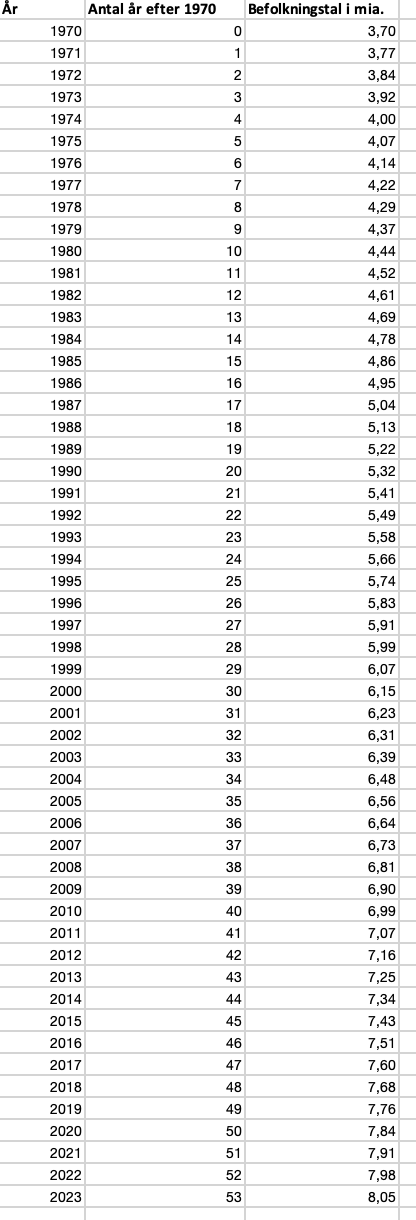
-
b) Har du husket titel og aksetitler?
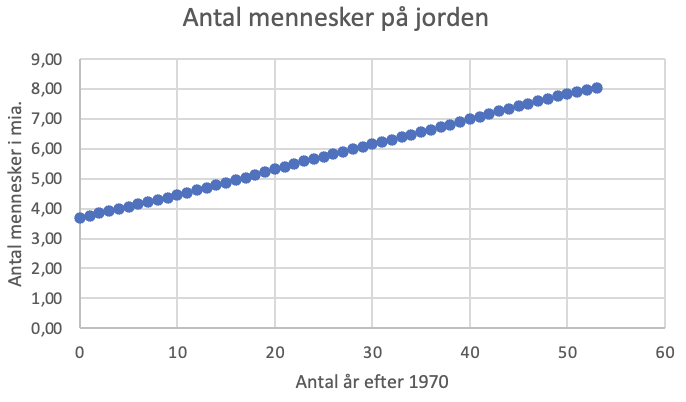
-
c) Modellen er \(y=0{,}0838x+3{,}6376\), hvor \(y\) er befolkningstallet i mia. og \(x\) er antal år efter 2019. Punkterne ligger nærmest perfekt på
linjen og \(R^2=0{,}9997\), så modellen giver en god beskrivelse af data.
-
d) Tallet \(0{,}0838\) betyder, at der har været en stigning på \(0{,}0838\) mia. mennesker om året. Dvs. at der hvert år kommer \(84\) mio.
mennesker mere på jorden. Ikke så mærkeligt, at vi får problemer med global warming osv. De \(3{,}6376\) betyder at der var \(3{,}6\) mio. mennesker på jorden i 1970 ifølge modellen.
-
e) År 2046.
Det er vigtigt at bemærke, at den type modeller, vi kigger på her, har en begrænset levetid. Det kan godt være, at der har været en lineær vækst i jordens befolkning de sidste 50 år, men det betyder ikke at væksten også vil være
lineær de næste 50 år. Derfor bør man være forsigtig med at bruge den slags modeller til at fremskrive udviklinger. Faktisk kan man allerede fornemme et lille dyk i befolkningsvæksten... Spørgsmålet er om det tilfældigt eller en
tendens? Det vil de kommende år vise.
Øvelse 3.6.5
Så befolkningstilvæksten er lineær... men hvor længe mon?
Ekstra
I dette ekstraafsnit skal vi først se på, hvordan man laver lineær regression i GeoGebra. Der er både fordele og ulemper ved GeoGebra, og derfor er det godt at kunne lave regression i både Excel og GeoGebra. Derefter vil vi se på
matematikken bag lineær regression.
Lineær regression i GeoGebra
Hvis du har problemer med følge guiden, så gør vinduet større. GeoGebra gemmer knapper, hvis vinduet er for småt
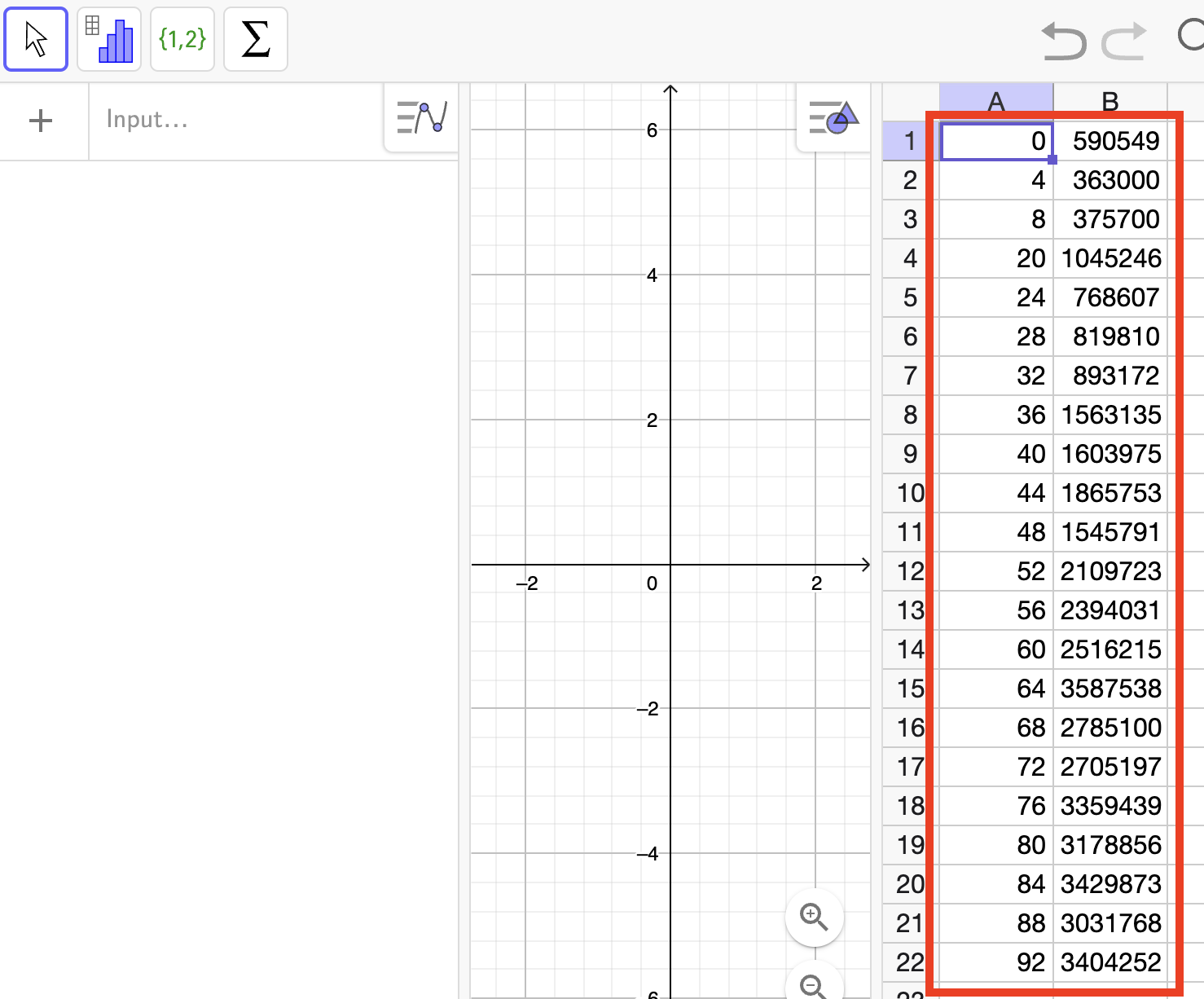
Vi kan lave lineær regression i GeoGebra også. Vi åbner GeoGebra og vælger ”Regneark”
Vi copy-paster nu data ind i regnearket. Her er det vigtigt at du højreklikker og vælger indsæt. Trykker du cmd-v (ctrl-v i Windows) virker det ikke:
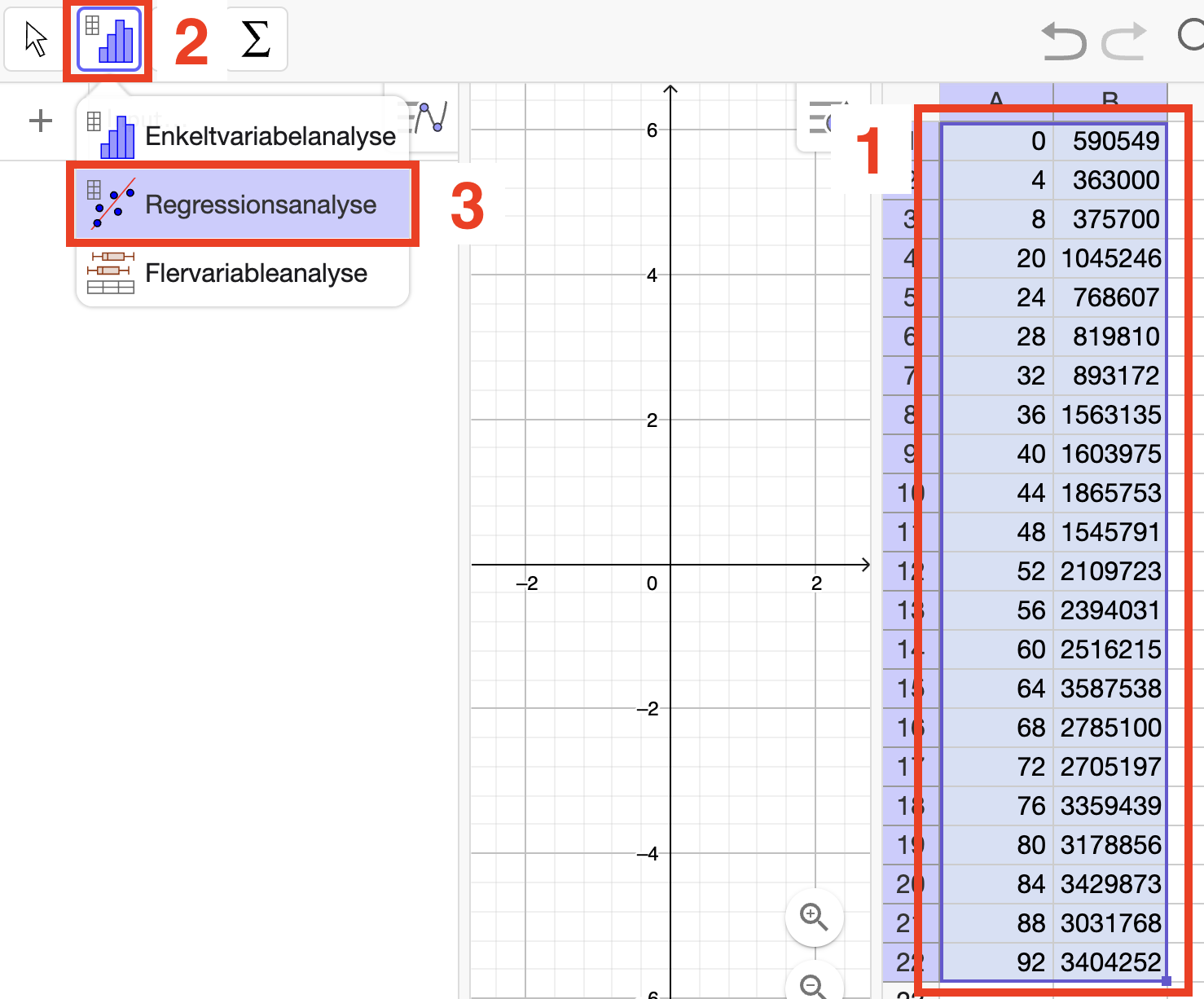
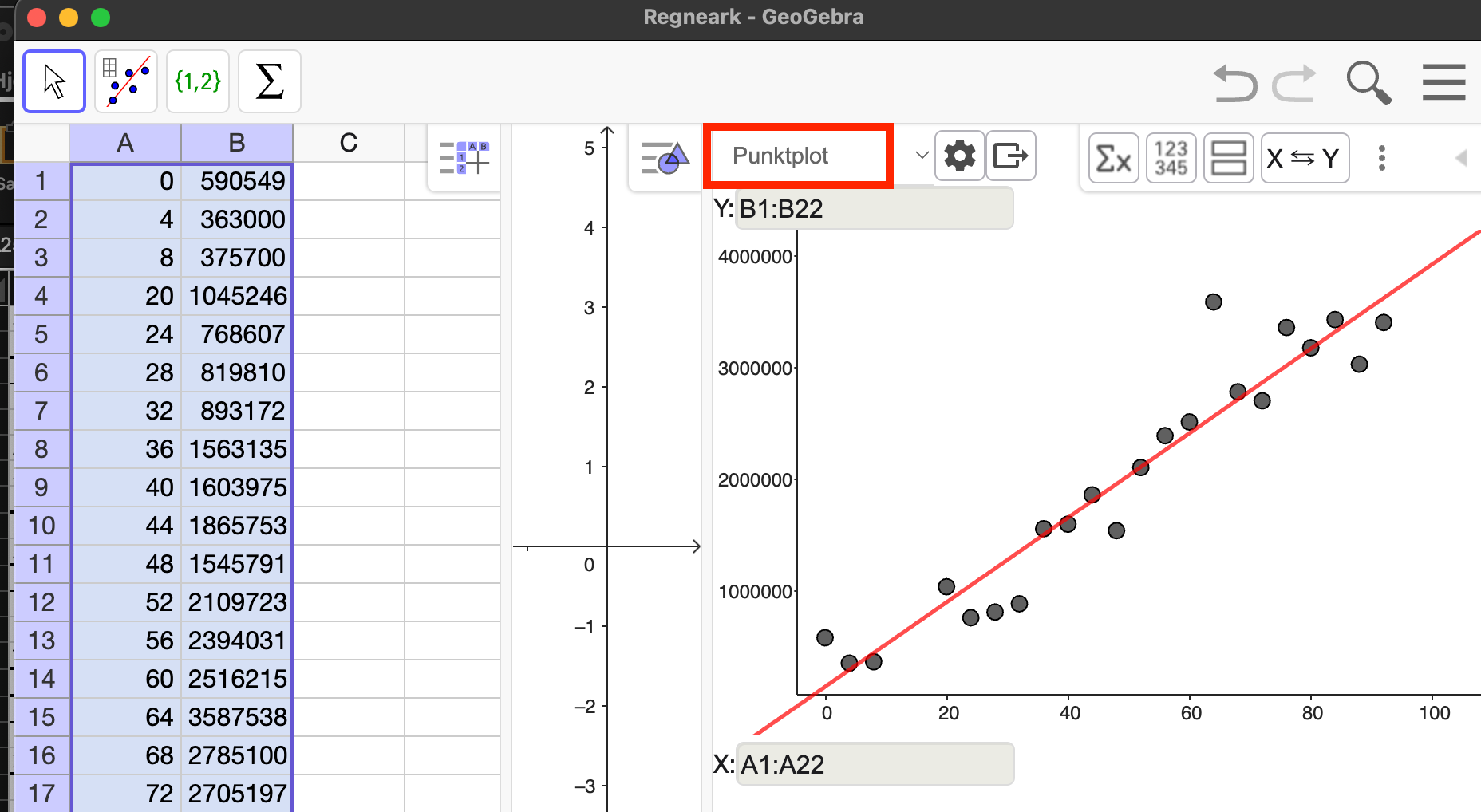
Vi rammer data ind og vælger ”Regressionsanalyse”
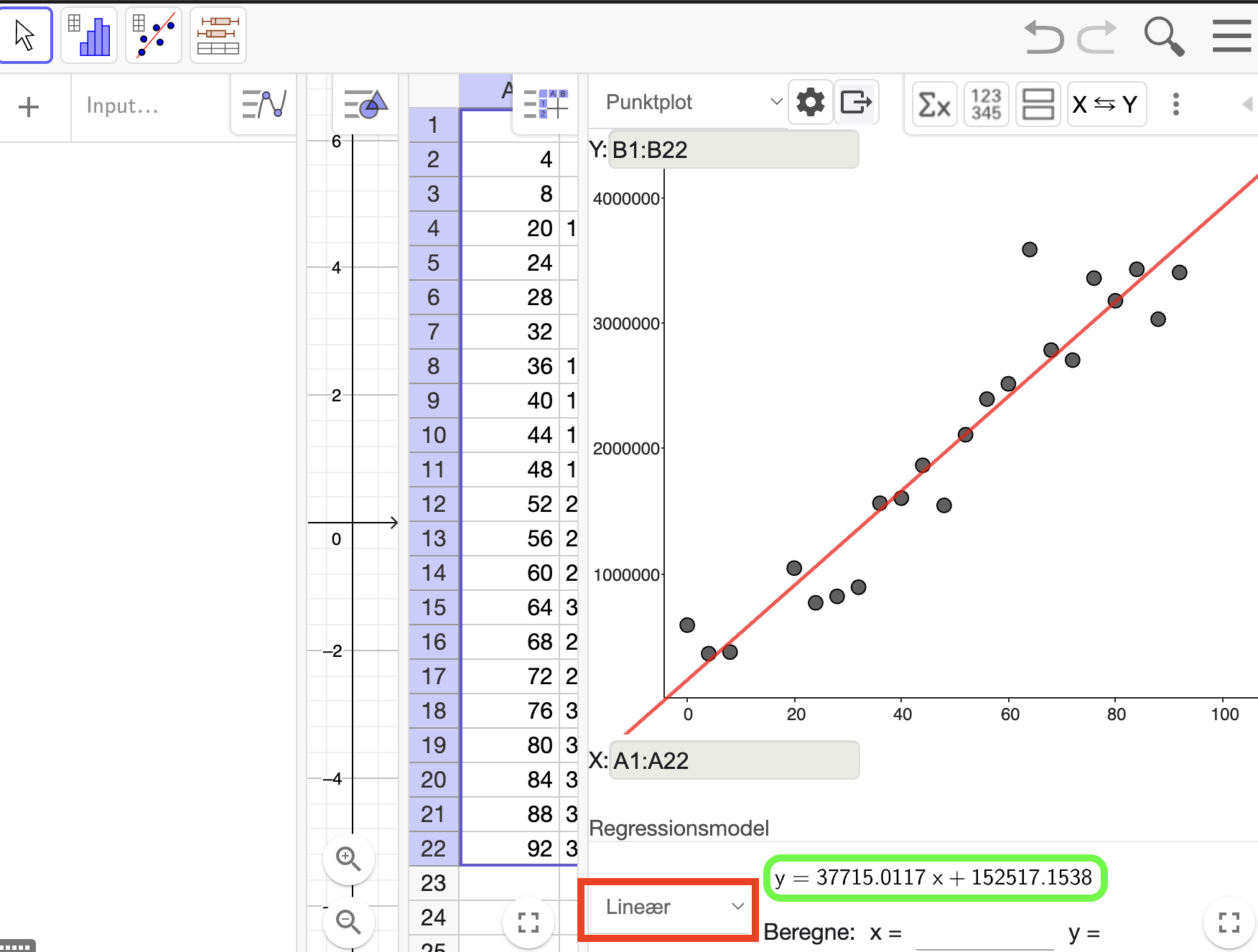
Vi vælger en ”Lineær” som Regressionsmodel:
Og vi ser at vores model er:
\[y=37715x+152517\]
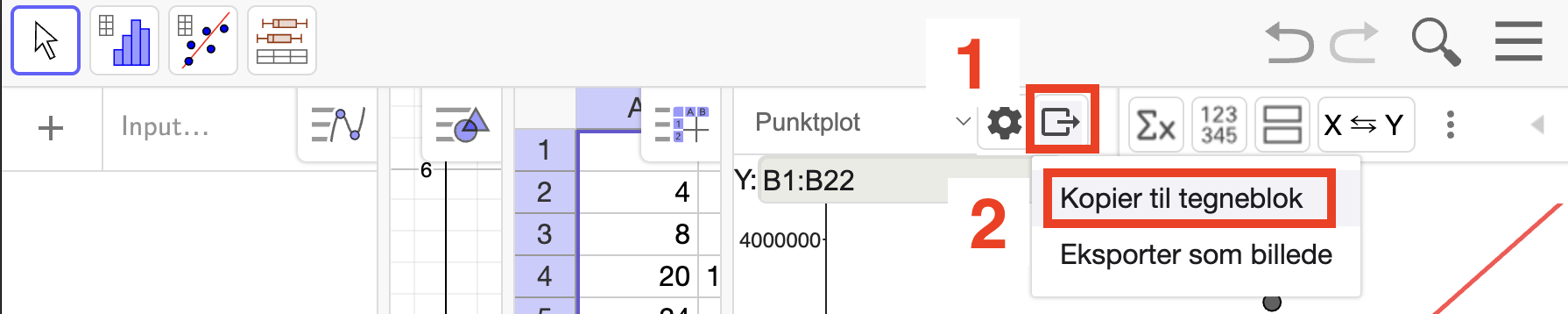
Men løjerne stopper ikke her. Vi kan få modellen ind i et algebravindue, så vi kan arbejde videre med den. Vælg ”Kopier til tegneblok”.
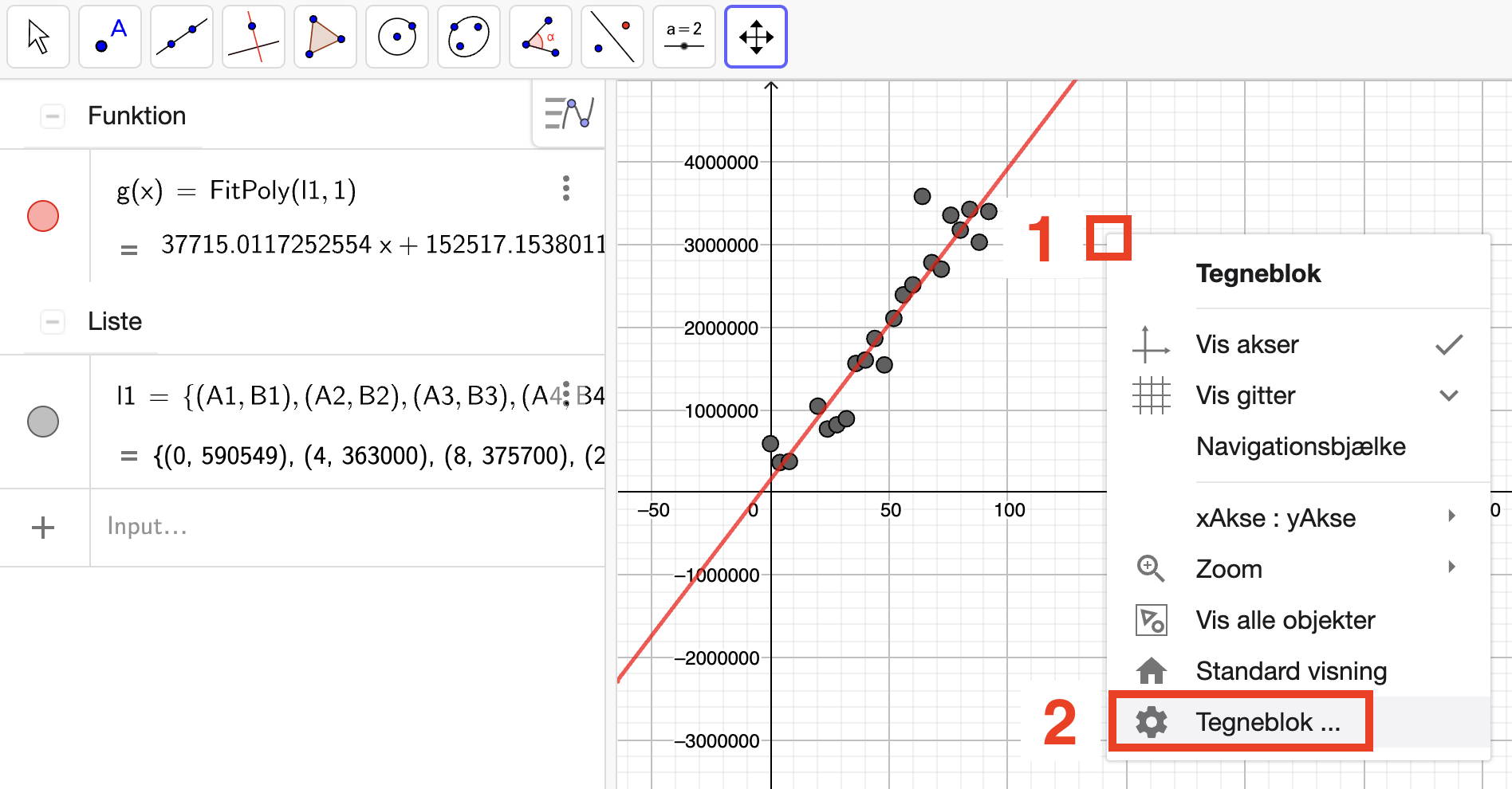
Vi lukker nu nogle vinduer og zoomer på akserne og får:
Funktionen \(g(x)\) kan vi arbejde med, som enhver anden funktion i GeoGebra.
Vi kan lave et xy-plot som egner sig til præsentation også. Vi skal bare indsætte titler på akserne. Vi højreklikker på et tomt stedet i koordinatsystemet og vælger ”Tegneblok ...”:
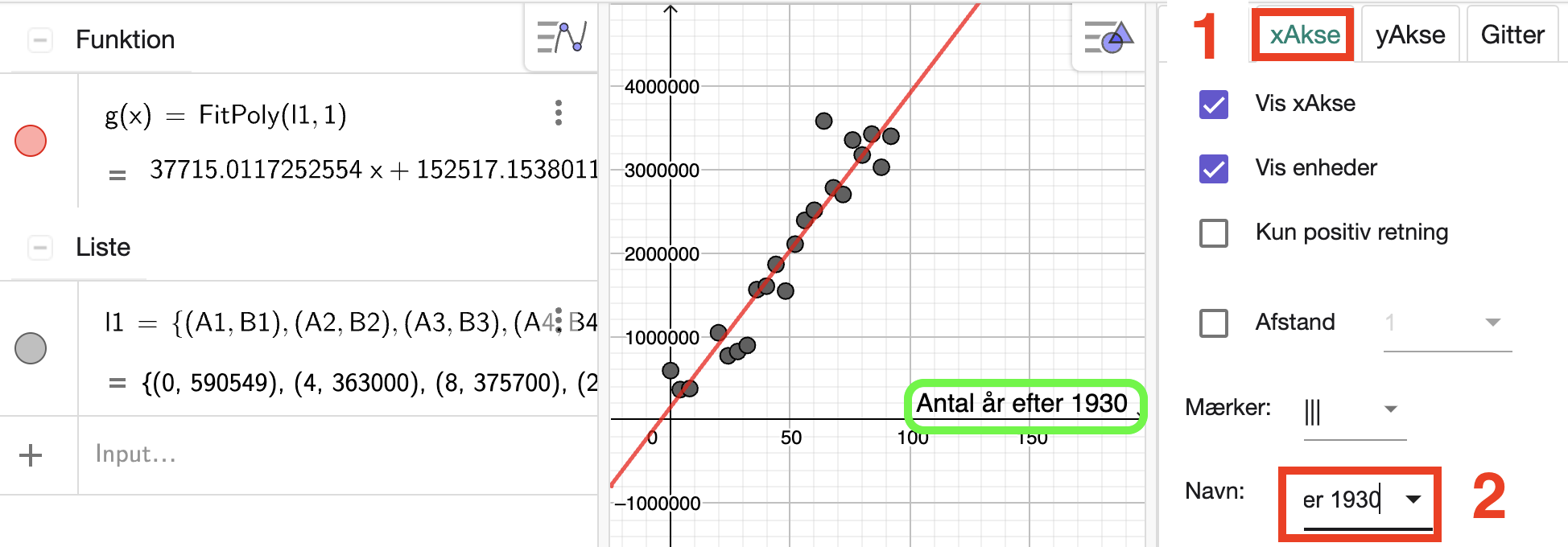
Vi trykker ”xAkse” og skriver ”Antal år efter 1930” ind under ”Navn”:
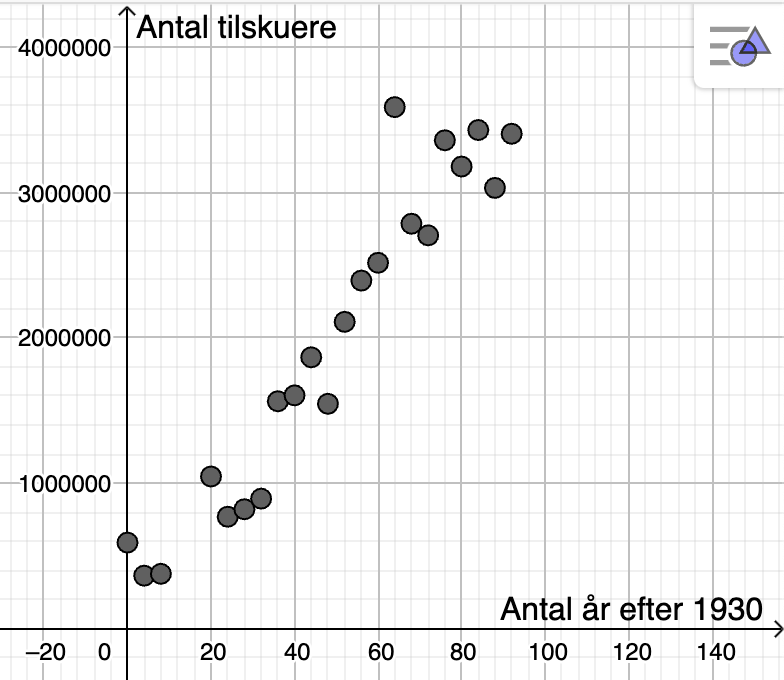
Vi tilføjer en titel på \(y\)-aksen på tilsvarende måde. Vi slukker for modellen (klikker på den røde bolle foran \(g(x)\)) og zoomer lidt så det er pænt:
og der var så det mine damer og herre. Et xy-plot i GeoGebra!
Det er klart at det er hurtigst at lave xy-plot i Excel, men skal man regne videre med modellen er GeoGebra smartere. Det skal dog nævnes at GeoGebra ikke virker med store datasæt (jeg tror vist grænsen er 350 rækker), så hvis
du har rigtig mange observationer, skal du bruge Excel.
For elever på den nye ordning (eller elever på A-niveau), kan jeg nævne, at der også kan laves residualplot i GeoGebra. Man laver det ud fra xy-plottet ved at klikke på ”Punktplot” og vælge ”residualdiagram”:
Sådan virker lineær regression
Vi skal nu se, hvordan den lineære model fremkommer når man laver regression i Excel og GeoGebra. Vi tager udgangspunkt i et simpelt xy-plot med kun tre punkter:
Vi tegner nu (bare så godt vi kan) en lineær funktion der bedst muligt går igennem punkterne. Det er svært, da punkter ikke rigtigt ligger på en linje:
Vi markerer nu den lodrette afstand mellem punkt og linje:
Afstandene repræsenterer fejlen mellem model og data for det pågældende punkt. Man kunne godt tro, at vi nu prøvede at minimere denne afstand. Altså at vi justerede linjen indtil, at den samlede lodrette afstand fra punkterne til
linjen var mindst muligt. Men det er ikke helt det vi gør. I stedet tegner vi kvadrater med afstandene som sidelængder:

Det er arealet af disse kvadrater som Excel/GeoGebra minimerer, når vi laver lineær regression. Altså Excel/GeoGebra justerer på linjen indtil, det samlede areal af kvadraterne ikke kan blive mindre. Vores model er så den linje,
som er resultatet af dette. Man kan undrer sig over, hvorfor det er arealerne og ikke afstandene der skal minimeres, men svaret er desværre uden for rækkevidde her på HHX. Faktisk er det tvivlsomt om metoden overhovedet er den
optimale i forhold til de konkrete eksempler i dette afsnit, men igen... denne bekymring hører ikke til på HHX. Så hermed en opfordring til at studere statistik på universitetet, så kan du komme og fortælle mig alt, hvad der er galt
med dette afsnit.