MATHHX B
\(\newcommand{\footnotename}{footnote}\)
\(\def \LWRfootnote {1}\)
\(\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#1}}}\)
\(\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}\)
\(\let \LWRorighspace \hspace \)
\(\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }\)
\(\newcommand {\mathnormal }[1]{{#1}}\)
\(\newcommand \ensuremath [1]{#1}\)
\(\newcommand {\LWRframebox }[2][]{\fbox {#2}} \newcommand {\framebox }[1][]{\LWRframebox } \)
\(\newcommand {\setlength }[2]{}\)
\(\newcommand {\addtolength }[2]{}\)
\(\newcommand {\setcounter }[2]{}\)
\(\newcommand {\addtocounter }[2]{}\)
\(\newcommand {\arabic }[1]{}\)
\(\newcommand {\number }[1]{}\)
\(\newcommand {\noalign }[1]{\text {#1}\notag \\}\)
\(\newcommand {\cline }[1]{}\)
\(\newcommand {\directlua }[1]{\text {(directlua)}}\)
\(\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}\)
\(\newcommand {\protect }{}\)
\(\def \LWRabsorbnumber #1 {}\)
\(\def \LWRabsorbquotenumber "#1 {}\)
\(\newcommand {\LWRabsorboption }[1][]{}\)
\(\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }\)
\(\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }\)
\(\def \mathcode #1={\mathchar }\)
\(\let \delcode \mathcode \)
\(\let \delimiter \mathchar \)
\(\def \oe {\unicode {x0153}}\)
\(\def \OE {\unicode {x0152}}\)
\(\def \ae {\unicode {x00E6}}\)
\(\def \AE {\unicode {x00C6}}\)
\(\def \aa {\unicode {x00E5}}\)
\(\def \AA {\unicode {x00C5}}\)
\(\def \o {\unicode {x00F8}}\)
\(\def \O {\unicode {x00D8}}\)
\(\def \l {\unicode {x0142}}\)
\(\def \L {\unicode {x0141}}\)
\(\def \ss {\unicode {x00DF}}\)
\(\def \SS {\unicode {x1E9E}}\)
\(\def \dag {\unicode {x2020}}\)
\(\def \ddag {\unicode {x2021}}\)
\(\def \P {\unicode {x00B6}}\)
\(\def \copyright {\unicode {x00A9}}\)
\(\def \pounds {\unicode {x00A3}}\)
\(\let \LWRref \ref \)
\(\renewcommand {\ref }{\ifstar \LWRref \LWRref }\)
\( \newcommand {\multicolumn }[3]{#3}\)
\(\require {textcomp}\)
\(\require {colortbl}\)
\(\let \LWRorigcolumncolor \columncolor \)
\(\renewcommand {\columncolor }[2][named]{\LWRorigcolumncolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\let \LWRorigrowcolor \rowcolor \)
\(\renewcommand {\rowcolor }[2][named]{\LWRorigrowcolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\let \LWRorigcellcolor \cellcolor \)
\(\renewcommand {\cellcolor }[2][named]{\LWRorigcellcolor [#1]{#2}\LWRabsorbtwooptions }\)
\(\newcommand {\tothe }[1]{^{#1}}\)
\(\newcommand {\raiseto }[2]{{#2}^{#1}}\)
\(\newcommand {\LWRsiunitxEND }{}\)
\(\def \LWRsiunitxang #1;#2;#3;#4\LWRsiunitxEND {\ifblank {#1}{}{\num {#1}\degree }\ifblank {#2}{}{\num {#2}^{\unicode {x2032}}}\ifblank {#3}{}{\num {#3}^{\unicode {x2033}}}}\)
\(\newcommand {\ang }[2][]{\LWRsiunitxang #2;;;\LWRsiunitxEND }\)
\(\def \LWRsiunitxdistribunit {}\)
\(\newcommand {\LWRsiunitxENDTWO }{}\)
\(\def \LWRsiunitxprintdecimalsubtwo #1,#2,#3\LWRsiunitxENDTWO {\ifblank {#1}{0}{\mathrm {#1}}\ifblank {#2}{}{{\LWRsiunitxdecimal }\mathrm {#2}}}\)
\(\def \LWRsiunitxprintdecimalsub #1.#2.#3\LWRsiunitxEND {\LWRsiunitxprintdecimalsubtwo #1,,\LWRsiunitxENDTWO \ifblank {#2}{}{{\LWRsiunitxdecimal }\LWRsiunitxprintdecimalsubtwo
#2,,\LWRsiunitxENDTWO }}\)
\(\newcommand {\LWRsiunitxprintdecimal }[1]{\LWRsiunitxprintdecimalsub #1...\LWRsiunitxEND }\)
\(\def \LWRsiunitxnumplus #1+#2+#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxprintdecimal {#1}}{\ifblank {#1}{\LWRsiunitxprintdecimal {#2}}{\LWRsiunitxprintdecimal {#1}\unicode
{x02B}\LWRsiunitxprintdecimal {#2}}}\LWRsiunitxdistribunit }\)
\(\def \LWRsiunitxnumminus #1-#2-#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumplus #1+++\LWRsiunitxEND }{\ifblank {#1}{}{\LWRsiunitxprintdecimal {#1}}\unicode {x02212}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\def \LWRsiunitxnumpmmacro #1\pm #2\pm #3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumminus #1---\LWRsiunitxEND }{\LWRsiunitxprintdecimal {#1}\unicode {x0B1}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\def \LWRsiunitxnumpm #1+-#2+-#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumpmmacro #1\pm \pm \pm \LWRsiunitxEND }{\LWRsiunitxprintdecimal {#1}\unicode {x0B1}\LWRsiunitxprintdecimal
{#2}\LWRsiunitxdistribunit }}\)
\(\newcommand {\LWRsiunitxnumscientific }[2]{\ifblank {#1}{}{\ifstrequal {#1}{-}{-}{\LWRsiunitxprintdecimal {#1}\times }}10^{\LWRsiunitxprintdecimal {#2}}\LWRsiunitxdistribunit }\)
\(\def \LWRsiunitxnumD #1D#2D#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumpm #1+-+-\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumd #1d#2d#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumD #1DDD\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumE #1E#2E#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumd #1ddd\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnume #1e#2e#3\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnumE #1EEE\LWRsiunitxEND }{\mathrm {\LWRsiunitxnumscientific {#1}{#2}}}}\)
\(\def \LWRsiunitxnumx #1x#2x#3x#4\LWRsiunitxEND {\ifblank {#2}{\LWRsiunitxnume #1eee\LWRsiunitxEND }{\ifblank {#3}{\LWRsiunitxnume #1eee\LWRsiunitxEND \times \LWRsiunitxnume
#2eee\LWRsiunitxEND }{\LWRsiunitxnume #1eee\LWRsiunitxEND \times \LWRsiunitxnume #2eee\LWRsiunitxEND \times \LWRsiunitxnume #3eee\LWRsiunitxEND }}}\)
\(\newcommand {\num }[2][]{\LWRsiunitxnumx #2xxxxx\LWRsiunitxEND }\)
\(\newcommand {\si }[2][]{\mathrm {\gsubstitute {#2}{~}{\,}}}\)
\(\def \LWRsiunitxSIopt #1[#2]#3{\def \LWRsiunitxdistribunit {\,\si {#3}}{#2}\num {#1}\def \LWRsiunitxdistribunit {}}\)
\(\newcommand {\LWRsiunitxSI }[2]{\def \LWRsiunitxdistribunit {\,\si {#2}}\num {#1}\def \LWRsiunitxdistribunit {}}\)
\(\newcommand {\SI }[2][]{\ifnextchar [{\LWRsiunitxSIopt {#2}}{\LWRsiunitxSI {#2}}}\)
\(\newcommand {\numlist }[2][]{\text {#2}}\)
\(\newcommand {\numrange }[3][]{\num {#2}\ \LWRsiunitxrangephrase \ \num {#3}}\)
\(\newcommand {\SIlist }[3][]{\text {#2}\,\si {#3}}\)
\(\newcommand {\SIrange }[4][]{\num {#2}\,#4\ \LWRsiunitxrangephrase \ \num {#3}\,#4}\)
\(\newcommand {\tablenum }[2][]{\mathrm {#2}}\)
\(\newcommand {\ampere }{\mathrm {A}}\)
\(\newcommand {\candela }{\mathrm {cd}}\)
\(\newcommand {\kelvin }{\mathrm {K}}\)
\(\newcommand {\kilogram }{\mathrm {kg}}\)
\(\newcommand {\metre }{\mathrm {m}}\)
\(\newcommand {\mole }{\mathrm {mol}}\)
\(\newcommand {\second }{\mathrm {s}}\)
\(\newcommand {\becquerel }{\mathrm {Bq}}\)
\(\newcommand {\degreeCelsius }{\unicode {x2103}}\)
\(\newcommand {\coulomb }{\mathrm {C}}\)
\(\newcommand {\farad }{\mathrm {F}}\)
\(\newcommand {\gray }{\mathrm {Gy}}\)
\(\newcommand {\hertz }{\mathrm {Hz}}\)
\(\newcommand {\henry }{\mathrm {H}}\)
\(\newcommand {\joule }{\mathrm {J}}\)
\(\newcommand {\katal }{\mathrm {kat}}\)
\(\newcommand {\lumen }{\mathrm {lm}}\)
\(\newcommand {\lux }{\mathrm {lx}}\)
\(\newcommand {\newton }{\mathrm {N}}\)
\(\newcommand {\ohm }{\mathrm {\Omega }}\)
\(\newcommand {\pascal }{\mathrm {Pa}}\)
\(\newcommand {\radian }{\mathrm {rad}}\)
\(\newcommand {\siemens }{\mathrm {S}}\)
\(\newcommand {\sievert }{\mathrm {Sv}}\)
\(\newcommand {\steradian }{\mathrm {sr}}\)
\(\newcommand {\tesla }{\mathrm {T}}\)
\(\newcommand {\volt }{\mathrm {V}}\)
\(\newcommand {\watt }{\mathrm {W}}\)
\(\newcommand {\weber }{\mathrm {Wb}}\)
\(\newcommand {\day }{\mathrm {d}}\)
\(\newcommand {\degree }{\mathrm {^\circ }}\)
\(\newcommand {\hectare }{\mathrm {ha}}\)
\(\newcommand {\hour }{\mathrm {h}}\)
\(\newcommand {\litre }{\mathrm {l}}\)
\(\newcommand {\liter }{\mathrm {L}}\)
\(\newcommand {\arcminute }{^\prime }\)
\(\newcommand {\minute }{\mathrm {min}}\)
\(\newcommand {\arcsecond }{^{\prime \prime }}\)
\(\newcommand {\tonne }{\mathrm {t}}\)
\(\newcommand {\astronomicalunit }{au}\)
\(\newcommand {\atomicmassunit }{u}\)
\(\newcommand {\bohr }{\mathit {a}_0}\)
\(\newcommand {\clight }{\mathit {c}_0}\)
\(\newcommand {\dalton }{\mathrm {D}_\mathrm {a}}\)
\(\newcommand {\electronmass }{\mathit {m}_{\mathrm {e}}}\)
\(\newcommand {\electronvolt }{\mathrm {eV}}\)
\(\newcommand {\elementarycharge }{\mathit {e}}\)
\(\newcommand {\hartree }{\mathit {E}_{\mathrm {h}}}\)
\(\newcommand {\planckbar }{\mathit {\unicode {x210F}}}\)
\(\newcommand {\angstrom }{\mathrm {\unicode {x212B}}}\)
\(\let \LWRorigbar \bar \)
\(\newcommand {\barn }{\mathrm {b}}\)
\(\newcommand {\bel }{\mathrm {B}}\)
\(\newcommand {\decibel }{\mathrm {dB}}\)
\(\newcommand {\knot }{\mathrm {kn}}\)
\(\newcommand {\mmHg }{\mathrm {mmHg}}\)
\(\newcommand {\nauticalmile }{\mathrm {M}}\)
\(\newcommand {\neper }{\mathrm {Np}}\)
\(\newcommand {\yocto }{\mathrm {y}}\)
\(\newcommand {\zepto }{\mathrm {z}}\)
\(\newcommand {\atto }{\mathrm {a}}\)
\(\newcommand {\femto }{\mathrm {f}}\)
\(\newcommand {\pico }{\mathrm {p}}\)
\(\newcommand {\nano }{\mathrm {n}}\)
\(\newcommand {\micro }{\mathrm {\unicode {x00B5}}}\)
\(\newcommand {\milli }{\mathrm {m}}\)
\(\newcommand {\centi }{\mathrm {c}}\)
\(\newcommand {\deci }{\mathrm {d}}\)
\(\newcommand {\deca }{\mathrm {da}}\)
\(\newcommand {\hecto }{\mathrm {h}}\)
\(\newcommand {\kilo }{\mathrm {k}}\)
\(\newcommand {\mega }{\mathrm {M}}\)
\(\newcommand {\giga }{\mathrm {G}}\)
\(\newcommand {\tera }{\mathrm {T}}\)
\(\newcommand {\peta }{\mathrm {P}}\)
\(\newcommand {\exa }{\mathrm {E}}\)
\(\newcommand {\zetta }{\mathrm {Z}}\)
\(\newcommand {\yotta }{\mathrm {Y}}\)
\(\newcommand {\percent }{\mathrm {\%}}\)
\(\newcommand {\meter }{\mathrm {m}}\)
\(\newcommand {\metre }{\mathrm {m}}\)
\(\newcommand {\gram }{\mathrm {g}}\)
\(\newcommand {\kg }{\kilo \gram }\)
\(\newcommand {\of }[1]{_{\mathrm {#1}}}\)
\(\newcommand {\squared }{^2}\)
\(\newcommand {\square }[1]{\mathrm {#1}^2}\)
\(\newcommand {\cubed }{^3}\)
\(\newcommand {\cubic }[1]{\mathrm {#1}^3}\)
\(\newcommand {\per }{\,\mathrm {/}}\)
\(\newcommand {\celsius }{\unicode {x2103}}\)
\(\newcommand {\fg }{\femto \gram }\)
\(\newcommand {\pg }{\pico \gram }\)
\(\newcommand {\ng }{\nano \gram }\)
\(\newcommand {\ug }{\micro \gram }\)
\(\newcommand {\mg }{\milli \gram }\)
\(\newcommand {\g }{\gram }\)
\(\newcommand {\kg }{\kilo \gram }\)
\(\newcommand {\amu }{\mathrm {u}}\)
\(\newcommand {\nm }{\nano \metre }\)
\(\newcommand {\um }{\micro \metre }\)
\(\newcommand {\mm }{\milli \metre }\)
\(\newcommand {\cm }{\centi \metre }\)
\(\newcommand {\dm }{\deci \metre }\)
\(\newcommand {\m }{\metre }\)
\(\newcommand {\km }{\kilo \metre }\)
\(\newcommand {\as }{\atto \second }\)
\(\newcommand {\fs }{\femto \second }\)
\(\newcommand {\ps }{\pico \second }\)
\(\newcommand {\ns }{\nano \second }\)
\(\newcommand {\us }{\micro \second }\)
\(\newcommand {\ms }{\milli \second }\)
\(\newcommand {\s }{\second }\)
\(\newcommand {\fmol }{\femto \mol }\)
\(\newcommand {\pmol }{\pico \mol }\)
\(\newcommand {\nmol }{\nano \mol }\)
\(\newcommand {\umol }{\micro \mol }\)
\(\newcommand {\mmol }{\milli \mol }\)
\(\newcommand {\mol }{\mol }\)
\(\newcommand {\kmol }{\kilo \mol }\)
\(\newcommand {\pA }{\pico \ampere }\)
\(\newcommand {\nA }{\nano \ampere }\)
\(\newcommand {\uA }{\micro \ampere }\)
\(\newcommand {\mA }{\milli \ampere }\)
\(\newcommand {\A }{\ampere }\)
\(\newcommand {\kA }{\kilo \ampere }\)
\(\newcommand {\ul }{\micro \litre }\)
\(\newcommand {\ml }{\milli \litre }\)
\(\newcommand {\l }{\litre }\)
\(\newcommand {\hl }{\hecto \litre }\)
\(\newcommand {\uL }{\micro \liter }\)
\(\newcommand {\mL }{\milli \liter }\)
\(\newcommand {\L }{\liter }\)
\(\newcommand {\hL }{\hecto \liter }\)
\(\newcommand {\mHz }{\milli \hertz }\)
\(\newcommand {\Hz }{\hertz }\)
\(\newcommand {\kHz }{\kilo \hertz }\)
\(\newcommand {\MHz }{\mega \hertz }\)
\(\newcommand {\GHz }{\giga \hertz }\)
\(\newcommand {\THz }{\tera \hertz }\)
\(\newcommand {\mN }{\milli \newton }\)
\(\newcommand {\N }{\newton }\)
\(\newcommand {\kN }{\kilo \newton }\)
\(\newcommand {\MN }{\mega \newton }\)
\(\newcommand {\Pa }{\pascal }\)
\(\newcommand {\kPa }{\kilo \pascal }\)
\(\newcommand {\MPa }{\mega \pascal }\)
\(\newcommand {\GPa }{\giga \pascal }\)
\(\newcommand {\mohm }{\milli \ohm }\)
\(\newcommand {\kohm }{\kilo \ohm }\)
\(\newcommand {\Mohm }{\mega \ohm }\)
\(\newcommand {\pV }{\pico \volt }\)
\(\newcommand {\nV }{\nano \volt }\)
\(\newcommand {\uV }{\micro \volt }\)
\(\newcommand {\mV }{\milli \volt }\)
\(\newcommand {\V }{\volt }\)
\(\newcommand {\kV }{\kilo \volt }\)
\(\newcommand {\W }{\watt }\)
\(\newcommand {\uW }{\micro \watt }\)
\(\newcommand {\mW }{\milli \watt }\)
\(\newcommand {\kW }{\kilo \watt }\)
\(\newcommand {\MW }{\mega \watt }\)
\(\newcommand {\GW }{\giga \watt }\)
\(\newcommand {\J }{\joule }\)
\(\newcommand {\uJ }{\micro \joule }\)
\(\newcommand {\mJ }{\milli \joule }\)
\(\newcommand {\kJ }{\kilo \joule }\)
\(\newcommand {\eV }{\electronvolt }\)
\(\newcommand {\meV }{\milli \electronvolt }\)
\(\newcommand {\keV }{\kilo \electronvolt }\)
\(\newcommand {\MeV }{\mega \electronvolt }\)
\(\newcommand {\GeV }{\giga \electronvolt }\)
\(\newcommand {\TeV }{\tera \electronvolt }\)
\(\newcommand {\kWh }{\kilo \watt \hour }\)
\(\newcommand {\F }{\farad }\)
\(\newcommand {\fF }{\femto \farad }\)
\(\newcommand {\pF }{\pico \farad }\)
\(\newcommand {\K }{\mathrm {K}}\)
\(\newcommand {\dB }{\mathrm {dB}}\)
\(\newcommand {\kibi }{\mathrm {Ki}}\)
\(\newcommand {\mebi }{\mathrm {Mi}}\)
\(\newcommand {\gibi }{\mathrm {Gi}}\)
\(\newcommand {\tebi }{\mathrm {Ti}}\)
\(\newcommand {\pebi }{\mathrm {Pi}}\)
\(\newcommand {\exbi }{\mathrm {Ei}}\)
\(\newcommand {\zebi }{\mathrm {Zi}}\)
\(\newcommand {\yobi }{\mathrm {Yi}}\)
\(\let \unit \si \)
\(\let \qty \SI \)
\(\let \qtylist \SIlist \)
\(\let \qtyrange \SIrange \)
\(\let \numproduct \num \)
\(\let \qtyproduct \SI \)
\(\let \complexnum \num \)
\(\newcommand {\complexqty }[3][]{(\complexnum {#2})\si {#3}}\)
\(\newcommand {\mleft }{\left }\)
\(\newcommand {\mright }{\right }\)
\(\newcommand {\mleftright }{}\)
\(\newcommand {\mleftrightrestore }{}\)
\(\require {gensymb}\)
\(\newcommand {\intertext }[1]{\text {#1}\notag \\}\)
\(\let \Hat \hat \)
\(\let \Check \check \)
\(\let \Tilde \tilde \)
\(\let \Acute \acute \)
\(\let \Grave \grave \)
\(\let \Dot \dot \)
\(\let \Ddot \ddot \)
\(\let \Breve \breve \)
\(\let \Bar \bar \)
\(\let \Vec \vec \)
\(\require {cancel}\)
\(\newcommand {\Dm }{\operatorname {Dm}}\)
\(\newcommand {\Vm }{\operatorname {Vm}}\)
\(\newcommand {\Var }{\operatorname {Var}}\)
\(\newcommand {\tcbset }[1]{}\)
\(\newcommand {\tcbsetforeverylayer }[1]{}\)
\(\newcommand {\tcbox }[2][]{\boxed {\text {#2}}}\)
\(\newcommand {\tcboxfit }[2][]{\boxed {#2}}\)
\(\newcommand {\tcblower }{}\)
\(\newcommand {\tcbline }{}\)
\(\newcommand {\tcbtitle }{}\)
\(\newcommand {\tcbsubtitle [2][]{\mathrm {#2}}}\)
\(\newcommand {\tcboxmath }[2][]{\boxed {#2}}\)
\(\newcommand {\tcbhighmath }[2][]{\boxed {#2}}\)
\(\newcommand {\toprule }[1][]{\hline }\)
\(\let \midrule \toprule \)
\(\let \bottomrule \toprule \)
\(\def \LWRbooktabscmidruleparen (#1)#2{}\)
\(\newcommand {\LWRbooktabscmidrulenoparen }[1]{}\)
\(\newcommand {\cmidrule }[1][]{\ifnextchar (\LWRbooktabscmidruleparen \LWRbooktabscmidrulenoparen }\)
\(\newcommand {\morecmidrules }{}\)
\(\newcommand {\specialrule }[3]{\hline }\)
\(\newcommand {\addlinespace }[1][]{}\)
\(\def \LWRsiunitxrangephrase { \protect \mbox {to (numerical range)} }\)
\(\def \LWRsiunitxdecimal {.}\)
9.2 Lineær programmering med niveaulinjer
I stedet for at regne alle punkterne i polygonområdet, kan vi bruge noget som hedder niveaulinjer til at finde det mest optimale punkt. Vi vil nu regne de samme eksempler/øvelser som i sidste afsnit, men bare med
niveaulinjer som en del af metoden.
En tøjproducent producerer trøjer og bukser.
Producenten har \(\SI {120}{m^2}\) bomuld og \(\SI {130}{m^2}\) polyester på lager.
Der går \(\SI {1,5}{m^2}\) bomuld og \(\SI {0,5}{m^2}\) polyester til en trøje.
Der går \(\SI {1}{m^2}\) bomuld og \(\SI {2}{m^2}\) polyester til et par et par bukser.
Dækningsbidraget er \(300\) kr. for en trøje og \(400\) kr. for et par bukser.
Hvor mange trøjer og hvor mange bukser skal der produceres få det størst mulige samlede dækningsbidrag? Hvad bliver det maksimale dækningsbidrag?
Opstilling af skema
Ingen ændringer her:
| . |
|---|
|
Trøjer |
Bukser |
Til rådighed |
| Bomuld |
\(\SI {1,5}{m^2}\) |
\(\SI {1}{m^2}\) |
\(\SI {120}{m^2}\) |
| Polyester |
\(\SI {0,5}{m^2}\) |
\(\SI {2}{m^2}\) |
\(\SI {130}{m^2}\) |
| Dækningsbidrag |
\(300\) kr. |
\(400\) kr. |
|
|
|
|
|
Kriteriefunktionen
Heller ingen ændringer her. Vi sætter altså
\(x=\) Antal producerede trøjer
\(y=\) Antal producerede bukser
Dækningsbidraget må dermed være givet ved:
\[f(x,y)=300x+400y\]
Polygonområde
Igen ingen ændringer. Ud fra skemaet ses at
\[1{,}5x+y\leq 120\]
For polyester må der gælde:
\[0{,}5x+2y\leq 130\]
Da vi ikke kan producerer et negativt antal trøjer eller bukser har vi:
\[x\geq 0 \quad \text {og}\quad y\geq 0\]
Disse uligheder kan vi skrive ind i et algebravindue i GeoGebra og det vil give os:
Det mørkeblå er polygonområdet.
Niveaulinjer
Nu kommer det nye. I stedet for at teste alle hjørnepunkterne i polygonområdet, vil vi starte med at identificere det optimale punkt. Det gør vi ved hjælp af det, som hedder niveaulinjer. En niveaulinje \(N(t)\) (læses ”n
t”) er en linje givet ved ligningen:
\[f(x,y)=t\]
Vi skal nu tegne to niveaulinjer i GeoGebra. Vi vælger (forklaring følger senere) \(N(20000)\) og \(N(30000)\). For at finde dem skal vi altså sætte \(f(x,y)=20000\) og \(f(x,y)=30000\). Det giver:
\[300x+400y=20000\quad \text {og} \quad 300x+400y=30000.\]
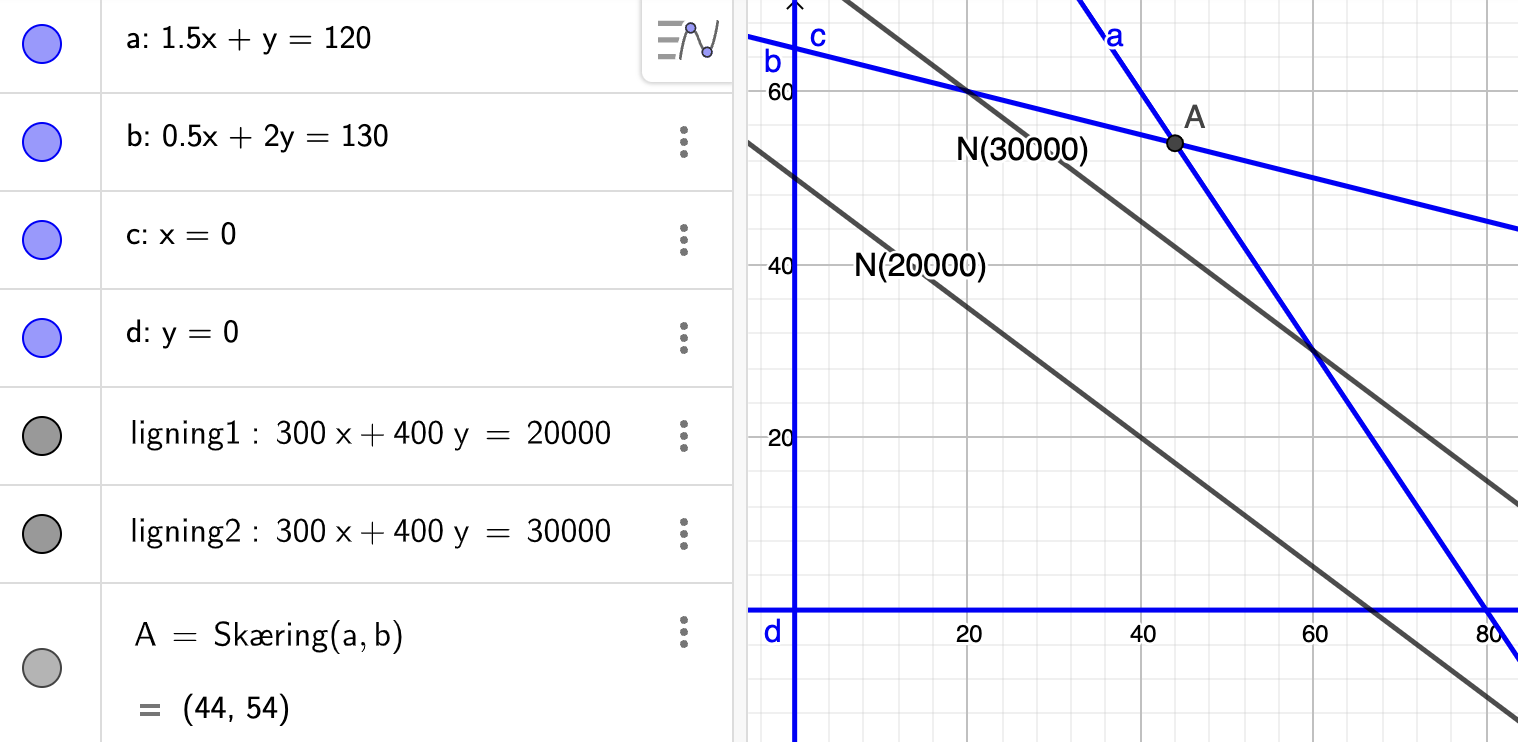
Vi taster disse to ligninger ind i GeoGebra (jeg har været inde og navngive linjerne, det sker ikke af sig selv):
De to linjer udtrykker to forskellige dækningsbidrag. Alle de punkter på \(N(20000)\) svarer til et dækningsbidrag på \(20000\) kr. og punkterne på \(N(30000)\) svarer til et dækningsbidrag på \(30000\) kr.
Vi ser at \(N(30000)\) fås ved at parallelforskyde \(N(20000)\) skråt op til højre. Vi får altså et højere dækningsbidrag (hvilket er det vi ønsker) når vi parallelforsker skråt op til højre. Vi forstiller os nu at vi bliver ved med at
forskyde \(N(20000)\) skråt op til højre. På et tidspunkt kommer linjen helt fri af polygonområdet. Det sidste punkt den slipper inden den forlader polygonområdet er det optimale punkt. Det er klart, at der må være tale om dette
her hjørnepunkt i polygonrådet:
Hvis du undrer dig over, hvor jeg fik \(20000\) og \(30000\) fra, så er svaret, at jeg prøvede mig frem, indtil jeg fandt to linjer, som lå pænt (adskilt) i polygonområdet.
Bestemmelse af det optimale punkt
Nu skal vi bare bestemme koordinaterne til det punkt, vi har fundet. Det gør vi ved at ændre ulighedstegnene til lighedstegn, og bruge skæringsværktøjet på det punkt, vi har identificeret:
Vi ser at skæringspunktet er \((44,54)\). Det betyder at vi skal producerer 44 trøjer og 54 bukser for at få det maksimale dækningsbidrag. Det maksimale dækningsbidrag finder vi ved at sætte punktet ind i \(f\):
\[f(44,54)=300\cdot 44+400\cdot 54=34800\]
Vi konkluderer at det optimale dækningsbidrag er \(34800\) kr.
Metoden virker måske lidt mere abstrakt end hjørneinspektion, men niveaulinjer er en essentiel del af lineær programmering som det forventes, at man har styr på. Man kan altså ikke vælge at sige ”Jeg holder mig til
hjørneinspektion”. Derudover er en god forståelse af niveaulinjer en forudsætning for at kunne mestre følsomhedsanalyse (Mat-A) og kvadratisk programmering (Mat-A).
Øvelse 9.2.1
En virksomhed producerer to produkter: Produk A og PRODUKT B.
Til PRODUKT A skal der bruges \(2\) arbejdstimer og \(\SI {5}{kg}\) råmateriale, mens PRODUKT B kræver \(4\) arbejdstimer og \(\SI {1}{kg}\) råmateriale.
Virksomheden har \(100\) arbejdstimer til rådighed og \(\SI {70}{kg}\) råmateriale.
Dækningsbidraget for PRODUKT A er \(10\) kr. pr. enhed mens det dækningsbidraget for PRODUKT B er \(8\) kr. pr. enhed.
Virksomheden vil gerne optimere dækningsbidraget.
-
a) Lav skema for oplysningerne, definer \(x\) og \(y\), opskriv en forskrift for kriteriefunktionen og tegn polygonområdet i GeoGebra. Det er samme
opgave som fra sidste afsnit, så du kan bruge det du lavede der, hvis du stadig har det.
-
b) Tegn to passende niveaulinjer. Dvs. du skal prøve dig lidt frem indtil du finder nogle niveaulinjer som ligger pænt i polygonområdet.
-
c) Bestem i hvilken retning dækningsbidraget vokser.
-
d) Identificer det optimale punkt (du skal ikke beregne det endnu). Argumenter for dit resultat.
-
e) Regn koordinaterne til det punkt du har identificeret som det optimale. Brug f.eks. skæringsværktøjet. Det er ikke nok at aflæse.
-
f) Bestem hvor mange PRODUKT A og hvor mange PRODUKT B virksomheden skal lave, og beregn det maksimale dækningsbidrag.
Løsning 9.2.1
-
a)
| . |
|---|
|
PRODUKT A |
PRODUKT B |
Til rådighed |
| Arbejdstimer |
\(\SI {2}{timer}\) |
\(\SI {4}{timer}\) |
\(\SI {100}{timer}\) |
| Råmateriale |
\(\SI {5}{kg}\) |
\(\SI {1}{kg}\) |
\(\SI {70}{kg}\) |
| Dækningsbidrag |
\(\SI {10}{kr}.\) |
\(\SI {8}{kr}.\) |
|
|
|
|
|
\(x\) er antal producerede PRODUKT A og \(y\) er antal producerede PRODUKT B. Forskriften er \(f(x,y)=10x+8y\) og polygonområdet er det mørkeste blå område.

-
b)

-
c) Vi kan se at niveauerne vokser i retning skråt til højre.
-
d) Ved at parallelforskyde niveaulinjerne skråt til højre indtil de slipper polygonområdet fås det optimale punkt:

-
e) Det optimale punkt har koordinaterne \((10,20)\).
-
f) Virksomheden skal producerer 10 PRODUKT A og 20 PRODUKT B, og det maksimale dækningsbidrag \(260\) kr.
-
Eksempel 9.2.1
Med udgangspunkt i virksomheden fra øvelsen ovenover forstiller vi os nu at dækningsbidraget for PRODUKT A falder til til 2 kr. pr. stk. Det giver følgende ændringer i kriteriefunktionen:
\[f(x,y)=2x+8y\]
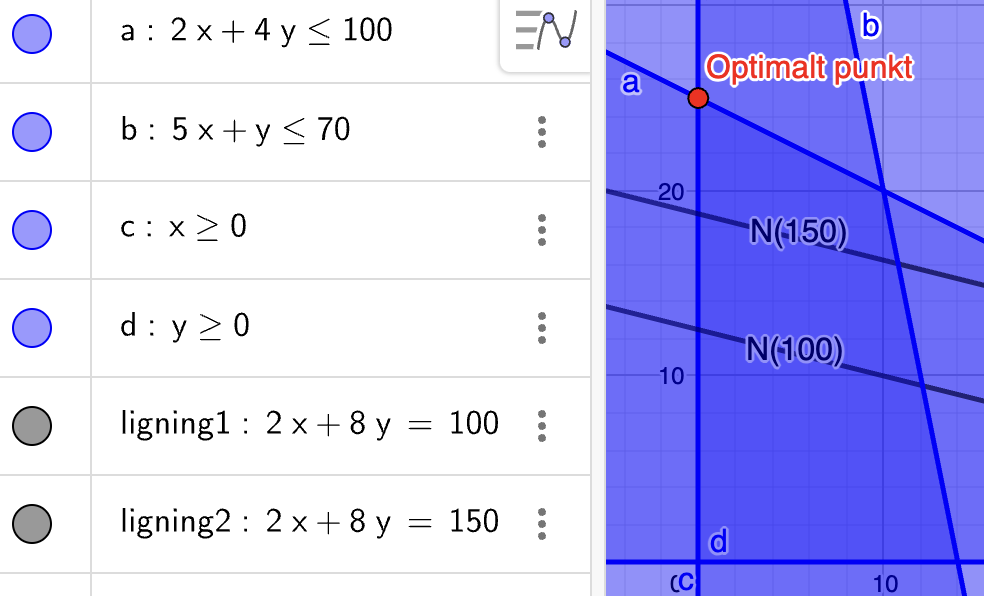
Vi tegner \(N(100)\) og \(N(150)\):
Vi ser at niveauerne stadig vokser skråt op til højre (mere op end til højre denne gang), og vi ser at det sidste punkt niveaulinjerne slipper være:
Aha! et nyt optimalt punkt! Punktets koordinater findes på sædvanligvis ved at ændre ulighedstegn til lighedstegn og bruge skæringsværktøjet.. Det optimale punkt bliver således \((0,25)\). Vi konkludere at dækningsbidraget for
PRODUKT A er blevet så lavt, at det ikke længere kan betale sig at producere PRODUKT A. Det maksimale dækningsbidrag regnes ved:
\[f(0,25)=2\cdot 0 + 8\cdot 25=200\]
Altså er det optimale dækningsbidrag 200 kr. ved en produktion af \(25\) PRODUKT B.
Øvelse 9.2.2
Vi bliver ved virksomheden fra eksemplet oven over. Bestem vha. niveaulinjer det optimale punkt når:
-
a) Dækningsbidraget for PRODUKT A er 10 kr. pr. stk. og dækningsbidraget for PRODUKT B er 5 kr. pr. stk.
-
b) Dækningsbidraget for PRODUKT A er 30 kr. pr. stk. og dækningsbidraget for PRODUKT B er 2 kr. pr. stk.
-
c) Dækningsbidraget for PRODUKT A er 4 kr. pr. stk. og dækningsbidraget for PRODUKT B er 16 kr. pr. stk.
Løsning 9.2.2
-
a) \((10,20)\)
-
b) \((14,0)\)
-
c) \((0,25)\)
-
Eksempel 9.2.2
Vi vil minimere funktionen \(f(x,y)=3x+2y\) underlagt betingelserne:
\(\seteqnumber{0}{9.}{0}\)
\begin{align*}
2x+y & \geq 10\\ x+y & \geq 8 \\ x+2y & \geq 10 \\ x & \geq 0 \\ y & \geq 1
\end{align*}
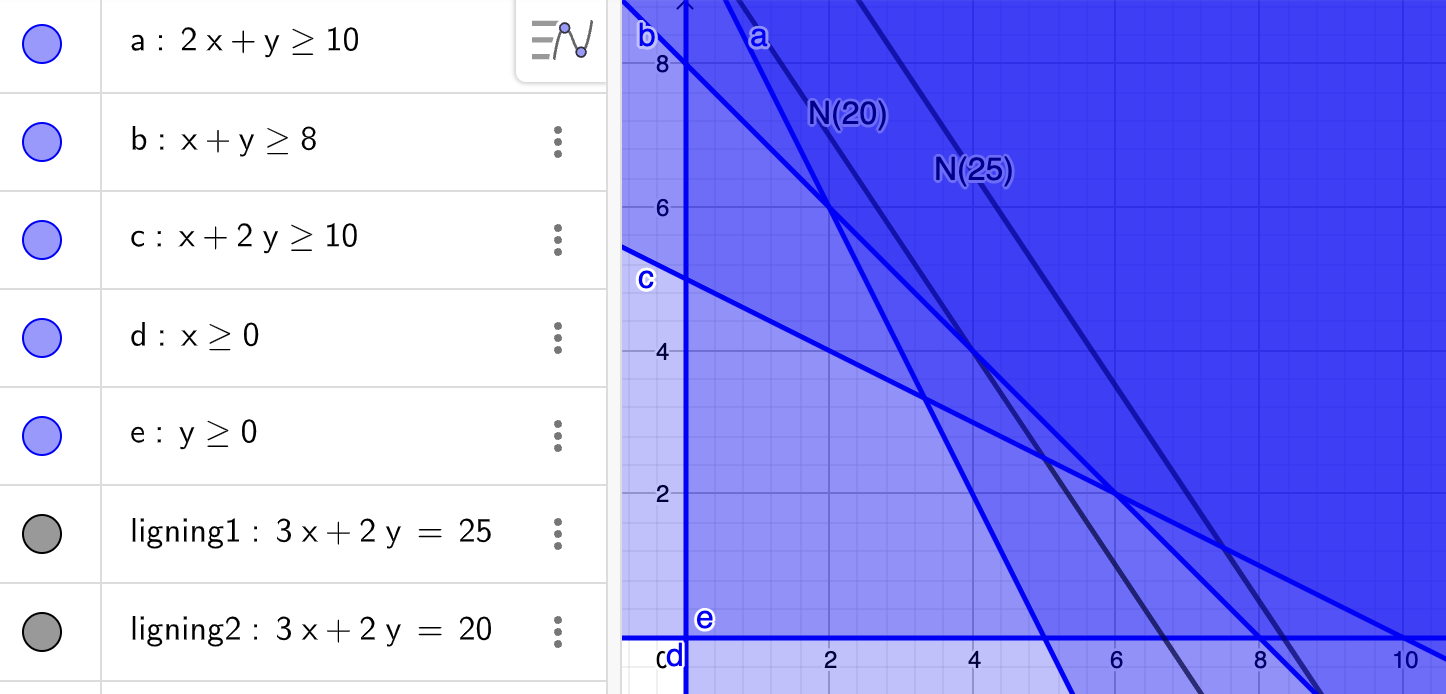
Vi tegner polygonområdet i GeoGebra og niveaulinjerne \(N(20)\) og \(N(25)\)
Vi ser at niveauerne vokser skråt op til højre. Vi er interesserede i minimum så vi skal altså forskyde niveaulinjerne i modsat retning – altså skråt ned til venstre. Vi ser at niveaulinjerne slipper polygonområdet i punktet \((2,6)\)
(vi tjekker at det er de eksakte koordinater ved at bruge skæringsværktøjet efter at vi har ændret ulighedstegn til lighedstegn). Vi regner funktionsværdien i punktet:
\[f(2,6)=3 \cdot 2+ 6 \cdot 2 = 18\]
Vi konkluderer at funktionen har minimum i \((2,6)\) og minimumsværdien er \(18\).
Øvelse 9.2.3
En elev vil sælge slikposer i kantinen. Han reklamere med:
Billige slikposer. Kom og køb. Du får miniskumbananer og/eller piratos. Mindst 20 stykker slik i hver pose. Mindst 120g i posen!
En miniskumbanan vejer \(9\) gram og en piratos vejer \(4\) gram.
Eleven kan indkøbe miniskumbananer til \(2\) kr. pr. stk. og piratos til \(50\) øre pr. stk.
Eleven vil gerne minimere sine omkostninger.
-
a) Lav et skema med oplysningerne i opgaven.
-
b) Definer \(x\) og \(y\).
-
c) Opskriv en funktion som udtrykker elevens omkostninger pr. slikpose.
-
d) Bestem vha. niveaulinjemetoden, hvad eleven skal putte i poserne og bestem den samlede udgift pr. pose.
-
e) Pludselig falder prisen på miniskumbananer til 0,75 kr. stk.. Hvad skal hun nu putte i poserne for at minimere sine udgifter. Brug igen niveaulinjer til
at svare på spørgsmålet.
Løsning 9.2.3
-
a)
| . |
|---|
|
Miniskumbananer |
Piratos |
Minimumskrav |
| Antal |
\(1\) |
\(1\) |
\(20\) |
| Vægt |
\(\SI {9}{g}\) |
\(\SI {4}{g}\) |
\(\SI {120}{g}\) |
| Omkostninger |
\(\SI {2}{kr}.\) |
\(\SI {0{,}5}{kr}.\) |
|
|
|
|
|
-
b) \(x\) er antal miniskumbananer i posen og \(y\) er antal piratos.
-
c) \(f(x,y)=2x+0{,}5y\)
-
d) Hun skal putte \(30\) piratos (og ingen miniskumbananer) i hver pose og det vil koste hende \(15\) kr. pr. pose.
-
e) Hun skal putte \(8\) miniskumbananer og \(12\) piratos i hver pose og det vil koste hende 12 kr.